Risk Aversion and Max-Entropy
Posted: 2016-10-02.
I want to share a nice little problem that came up in discussion between Yiling Chen, Madhu Sudan, and myself. It turns out to have a cute solution that connects the geometry of proper scoring rules with a "max-entropy" rule.
A primer on proper scoring rules will be useful first!
The Tale of Rita
Once upon a time, Risk-Averse Rita worked as a weather reporter in Incentiveland playing the following game each day:
- Rita is given a set $Q$ of possible probability distributions over the day's weather outcome, e.g. $Q \subseteq \Delta_{\{\text{rain, cloud, sun}\}}$.
- Rita makes a prediction $p$, a distribution over the day's weather outcome.
- Nature picks a true distribution $q$ from $Q$, perhaps adversarially depending on Rita's prediction.
- The true weather outcome $e$ is drawn according to $q$.
- Rita is scored with a proper scoring rule $S(p,e)$.
In the case where $|Q| = 1$, i.e. Rita knows the true distribution $q$ of nature, then properness of the scoring rule implies that she should just report $q$. Now, if Rita is risk averse and wishes to maximizes her minimum expected score, how should she play? In math, she wants to solve
\[ \max_p \min_{q \in Q} \mathbb{E}_{e\sim q} S(p, e) . \] Recalling the notation $S(p;q)$ for expected score of report $p$ when $e \sim q$, this is \[ \max_p \min_{q \in Q} S(p;q) . \]The Solution
Luckily, Rita found an optimal strategy. The intuitive statement of the solution is:
If $Q$ is a convex set, then the optimal strategy is to assume the adversary will pick the "max-entropy" distribution in $Q$ and best-respond accordingly.
Furthermore, in this case, the adversary cannot improve on actually picking the "max-entropy" distribution.
Why do I have quotes around "max-entropy"? Because the measure of entropy changes depending on the scoring rule.
If you read my post on generalized entropies, you know that:
- Every proper scoring rule maps to a convex function $G$ where $G(q)$ is the expected score for optimally (truthfully) reporting given belief $q$.
- The concave function $F = -G$ can be interpreted as a "generalized entropy" function under an axiomatic approach.
Theorem. Let $Q$ be any convex set of distributions and suppose Rita faces scoring rule $S$ with differentiable convex expected score $G$. To solve the problem \[ \arg\max_p \min_{q \in Q} S(p;q) , \] Rita's optimal strategy is to report \[ q^* := \arg\min_{q \in Q} G(Q) . \]
Proof. It may be helpful to first see the pictures below. First, we will show that if Rita picks $p=q^*$, then her expected score is at least $G(q^*)$ for any choice of nature (achieved when nature chooses $q^*$). Then, we will show that any other report $p \neq q^*$ results in a worse score.
Claim 1. $\min_{q\in Q} S(q^*;q) = G(q^*)$.
Proof of claim: We just want to show for all $q \in Q$ \begin{align} S(q^*; q) - G(q^*) &\geq 0 \\ \iff ~ \langle dG(q^*), q-q^* \rangle &\geq 0 \end{align} using the scoring rule characterization $S(p;q) = G(p) + \langle dG(p), q-p \rangle$ where $dG(p)$ is the subgradient (i.e. gradient) of $G$ at point $p$.
Now we just want to prove $\langle dG(q^*), q-q^* \rangle \geq 0$ for all $q \in Q$. But since $G$ is differentiable, this is actually equal to the directional derivative of $G$ in the direction $q-q^*$: \[ \langle dG(q^*), q-q^* \rangle = \lim_{h\to 0} \frac{G(q^* + h(q-q^*)) - G(q^*)}{h} . \] Now, we assumed $Q$ is a convex set, and both $q^*,q \in Q$. So for every $0 \leq h \leq 1$, the point $q' := q^* + h(q-q^*)$ is in $Q$. Furthermore, since we assumed $q^* = \arg\min_{p \in Q} G(p)$, we have $G(q') - G(q) \geq 0$.
So the right side is a limit over nonnegative terms, so the left side cannot be negative.
Claim 2. For all $p$, $\min_{q \in Q} S(p;q) \leq G(q^*)$.
Proof of claim: In particular, $\min_{q \in Q} \leq S(p;q^*)$ because $q^* \in Q$. Now by definition of a proper scoring rule, $S(p;q^*) \leq S(q^*;q^*) = G(q^*)$.
Here we have a binary outcome problem, e.g. the weather is either sunny or not, with probability of sun on the horizontal axis. Plots the convex expected score function $G$ for a scoring rule $S$, and the convex set $Q$ of possible probability distributions of nature.
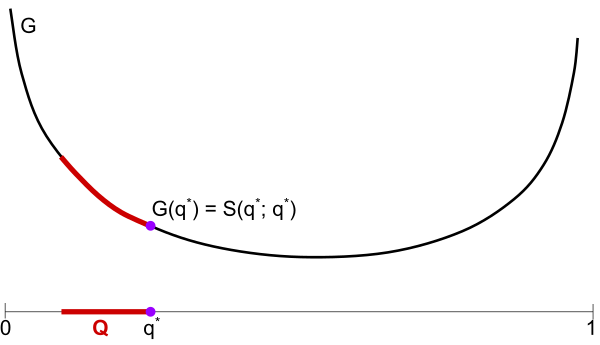
Above: $q^*$ is the "max-entropy" (minimum $G(q)$) among the set $Q$. I claim Rita should pick $q^*$.
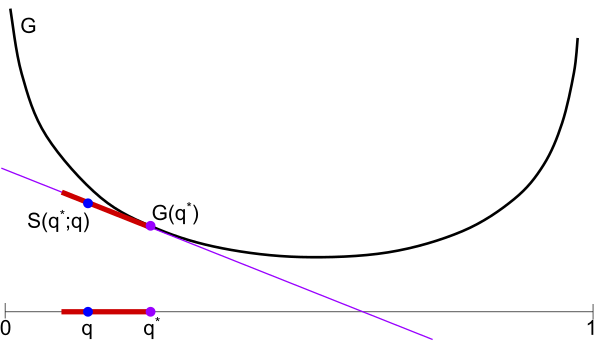
Below: Illustration of Claim 1. Supposing Rita reports $q^*$, then nature's best response is $q^*$, as any other choice $q \in Q$ results in a higher expected score $S(q^*;q)$. This shows Rita can achieve $G(q^*)$ by picking $q^*$.
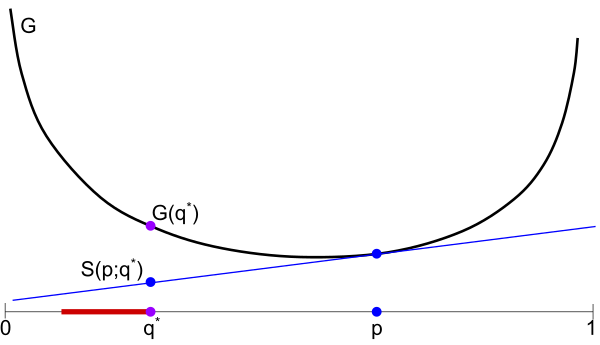
Below: Illustration of Claim 2. If Rita makes any other prediction $p \neq q^*$, nature can force her to achieve worse than $G(q^*)$ by picking $q^*$.
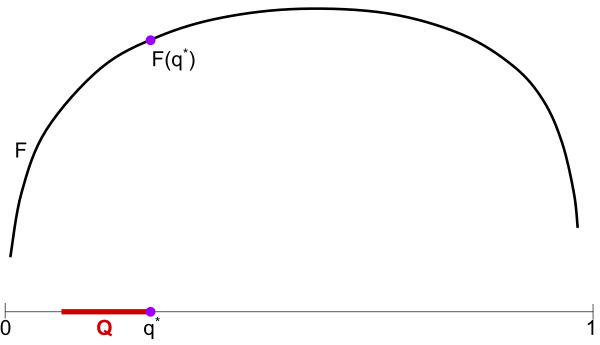
Below: By flipping $G$, we can view it as a generalized entropy $F$ where $q^*$ is the max-entropy distribution in $Q$.
Questions
Here are some exercises you might enjoy followed by open questions that would be nice to resolve, at least for Rita's sake.Exercise 1.
Rita's cousin, Risk-Neutral Rick, has a "meta-belief" in the form of a distribution $r$ over $Q$, i.e. $r$ assigns a probability to each $q \in Q$ as being the correct belief.
How should Rick report to maximize expected score, i.e. what $p$ solves
Exercise 2.
Suppose $Q$ is not a convex set; give a counterexample to the theorem.
Open question 1.
Suppose $Q$ is not a convex set.
I would guess that Rita's optimal report is the max-entropy $q$ in the convex hull of $Q$.
Prove me right, or disprove it and find Rita's optimal strategy instead.
Open question 2.
What if $G$ is convex, but not differentiable?
The theorem probably still holds, but the proof needs to be much more careful.
What happens when $G$ is non-differentiable is that, at some points $q$, there are multiple choices of subgradient $dG(q)$.
If we use the wrong one when constructing the scoring rule $S$, then the theorem won't hold; to see this, picture $G$ with a kink at its minimum (such as $G(x) = |x|$) and convince yourself that, if $Q$ contains a ball around the global minimum, then the subgradient chosen at the minimum must be $0$ for the theorem to hold.
Maybe elsewhere you don't need to be so careful, and can just use that the subgradients at $p$ form a convex set; I'm not sure.
Open question / challenge 3.
Extend this theorem, as far as possible, to the case of general decision problems rather than just proper scoring rules.

