Generalized Entropies and the Value of Information
Posted: 2016-09-24.
In this post, I'll discuss axioms for entropy functions that generalize Shannon entropy and connect them to the value of information for a rational decision maker. We'll see that convexity turns out to be a natural and simple axiom that nicely links the two settings.
Background
Shannon, in his 1948 paper "A Mathematical Theory of Communication" (which is definitely worth a read), addressed a beautiful question: How should we measure "how much information" is contained in a draw from a probability distribution $p$ over a finite set of outcomes?
Let us call a proposed measure $F(p)$ a generalized entropy. We commonly nowadays overload notation by writing $F(X)$ when $X$ is distributed according to $p$. If $X$ and $Y$ are jointly distributed according to $p$, we can write $F(X,Y) = F(p)$ and also write $F(X)$ for the entropy of the distribution over just $X$.
Some convenient notation: let $p_X$ be the distribution of $X$, $p_{X|y}$ the distribution of $X$ conditioned on $Y=y$, and so on.
Given proposed measure of uncertainty $F$, it is natural to immediately consider (as Shannon did in his paper) what happens if only part of the outcome or one of several random variables is revealed. Let us define the conditional (generalized) entropy to be the expected entropy: \[ F(X|Y) := \mathbb{E}_{y\sim Y} F(p_{X|y}) . \] The conditional entropy is the average entropy of $X$ after observing $Y$. Some use a different definition (the "other side" of the chain rule); I'll support my choice when we discuss value of information.
Shannon Axioms
Shannon proposed a reasonable-sounding set of axioms for such information measures:
- $F$ should be continuous in each $p_i$.
- When $p$ is uniform on support size $n$, $F$ should be monotonically increasing in $n$.
- (Chain rule) $F(X) + F(Y|X) = F(X,Y)$.
Naturally, since then, there has been interest in generalized entropies that do not necessarily satisfy all three axioms. The problem is that Axioms S1 and S2, while seemingly necessary, are too weak; satisfying only these two does not seem to qualify a function for generalized entropy status. But the third is too strong: add it in, and we are reduced to only $H$.
One Axiom to Rule Them All?
I'm going to shamelessly skip over other sets of proposed axioms and background on common entropy measures such as Rényi entropy. Instead, I'll propose an axiom that I haven't yet seen written anywhere, but I expect has probably been studied (please let me know if you have a reference!):
- $F(Y|X) \leq F(Y)$. That is, on average, more information reduces entropy.
My proposal is that axiom B1 is necessary and sufficient for $F$ to be considered a generalized entropy. Here I am intuitively thinking of entropy as a measure of uncertainty.
- If $F$ always diminishes on average when given information, then it seems fair to say that $F$ measures some sort of uncertainty.
- On the other hand, if there are situations where we expect for $F$ to be larger on average when gaining information, then $F$ does not seem to be measuring uncertainty.
If that's not compelling, then how about a more mathematical argument for B1?
Proposition 1. Axiom B1 is equivalent to concavity of $F$.
Proof. Recalling the definition of conditional entropy, Axiom B1 states \[ \mathbb{E}_{y\sim Y} F\left( p_{X|y} \right) ~ \leq F(p_Y) . \] An exercise for the reader is to check that $\mathbb{E}_{y\sim Y} \left[ p_{X|y} \right] = p_Y$. In other words, the expectation of a future posterior belief over $Y$ is always equal to the prior belief on $Y$.
But now we can see that Axiom B1 is no more than Jensen's inequality, so it is equivalent to concavity.
Corollary 1. Axiom B1 implies Axioms S1 and S2.
Concave functions are continuous on the interior of their domains (let's be a bit sloppy about the boundary), and Jensen's inequality covers S2.
Corollary 2. The Shannon entropy $H$ is the unique entropy function satisfying B1 and the chain rule.
Checking concavity of $H$ is left to the reader. Meanwhile, any function satisfying B1 and the chain rule satisfies all of Shannon's axioms, so must be $H$.
My belief in this axiom is strong enough that for the rest of this blog post (and perhaps for the rest of human history) I will say "generalized entropy function" to mean any function satisfying axiom B1.
Value of Information
In 1966, Ronald Howard proposed a way to assign value to pieces of information in the context of decisionmaking. "Information Value Theory" already contained references to the connection to Shannon's entropy, but I have yet to see his ideas written out more explicitly. (His paper seems difficult to find online, but a little birdie told me to check here.)
The idea is that an agent has to choose a decision $d$ from some set; simultaneously, nature will draw a realization $e$ of a random event $E$. The agent will receive utility $u(d,e)$.
Now, for any given distribution $p_E$ over $E$, let $d^*(p_E)$ denote the optimal decision to take if nature draws $E$ according to $p_E$. A decisionmaker having belief $p_E$ will make decision $d^*(p_E)$ and expects to get utility \[ G(p_E) = \mathbb{E}_{e \sim p_E} u(d^*(p_E), e) . \]
The nice thing about $G(p)$ is that it captures the "optimal expected utility" for a decisionmaker when she has different beliefs $p$ -- or more to the point, different pieces of information, as we'll see soon.
Proposition 2. For any decision problem, the corresponding "optimal expected utility" function $G$ is convex.
Proof. We can write $G$ as $G(p_E) = \max_d \mathbb{E}_{e\sim p_E} u(d, e)$. Then it becomes clear that $G$ is a pointwise maximum over linear functions (the expectation is a linear function of $p$), so $G$ is convex.
This should look familiar if you've seen proper scoring rules. Proper scoring rules are a special case where the decision is to pick a predicted probability distribution $p$ over the outcomes of $E$ and the utility function is $S(p,e)$. In fact, proper scoring rules give a converse:
Proposition 3. For any convex funtion $G: \Delta_E \to \mathbb{R}$, there exists a decision problem (in particular, a proper scoring rule) with "optimal expected utility" function $G$.
(See the post on proper scoring rules.)The idea in Howard's paper is to use $G$ to measure the "value" of information. To illustrate, let me define $G$ as the value-of-information function corresponding to $u$ and write it as $G(E)$. If the agent will observe the outcome of some $X$ prior to deciding, then she can make the decision $d^*(p_{E|x})$ and get expected utility \[ G(E|X) := \mathbb{E}_{x\sim X} G(p_{E|x}) . \] Of course, convexity of $G$ implies (and is equivalent to) $G(E|X) \geq G(E)$; this is the fact that more information always helps in decisionmaking.
Now, we can ask Howard's (very natural) question: How much does a decisionmaker value a new piece of information? The answer, of course, is the improvement it brings to expected utility. If she were risk-neutral, she would pay up to $G(E|X) - G(E)$ to observe $X$.
Now, the analogy I want to point out is with the reduction in uncertainty $X$ brings to an entropy function, $F(E) - F(E|X)$. Let's turn this analogy into a formal correspondence.
The Equivalence
Let me offer a formalization of what I believe was the broader idea of Howard's paper.
Theorem. Every generalized entropy $F$ corresponds to a decision problem such that the amount of uncertainty reduced by a piece of information is equal to a decisionmaker's marginal value for it.
Proof. $F$ is a concave function with the piece of information $X$ reducing uncertainty about $E$ by the amount $F(E) - F(E|X)$. (This is often called the "Jensen gap" as it is the violation in Jensen's inequality.) Decision problems are in one-to-one correspondence with convex functions $G$ with marginal value for information $G(E|X) - G(E)$. For the correspondence, we can just take $G = -F$.
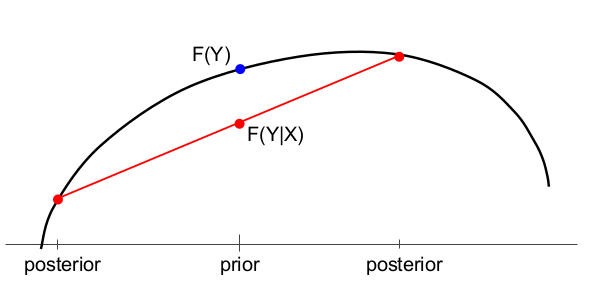
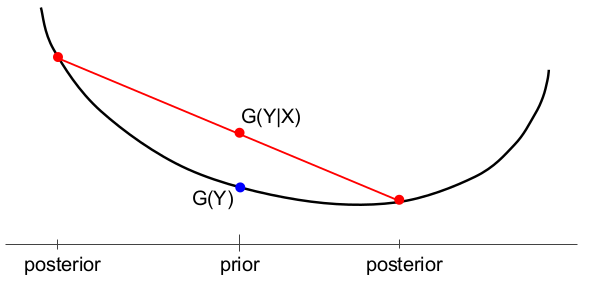
In both figures, $Y$ is a binary random variable with $\Pr[Y=1]$ on the horizontal axis. There is initially a prior probability, then two possible posteriors depending on the realization of the random variable $X$.
(Above) A generalized entropy function $F$ measuring uncertainty about $Y$ before ($F(Y)$) and after ($F(Y|X)$) observing a piece of information $X$.
(Below) The expected utility of a decisionmaker without ($G(Y)$) and with ($G(Y|X)$) the piece of information $X$.
Why Do We Need More Entropy?
Shannon entropy is a wonderful thing that has been proven to be the "right" notion in a huge number of contexts. Why should we use other entropies, and specifically, how can this help when applied to decisionmaking?
-- Priya (my wife)
The point I want to make is that often (including in many papers), we use entropy to measure how much information we've collected regardless of how we want to use that information. Let me illustrate with a parable.
Once upon a time, Ms. Cert and Ms. Tea lived together in the great state of New Jersey and commuted every day to work in Manhattan. Ms. Tea was calm and laid back, but Ms. Cert couldn't stand uncertainty. She was always tracking various weather forecasts over the entire Northeast. When the office ordered lunch from one of the 73 local pizza places, she needed to know immediately which one ("There are so many possibilities!").
But one morning Ms. Tea, normally so calm, rushed into the kitchen in a state of panic. "I heard the bridge might be closed today! We might be late for work! We have to find out if the bridge is closed!" Ms. Cert put down her coffee and looked up from the crossword. "Will you relax?" she said in an exasperated tone. "For goodness' sake, Ms. Tea, what's the big deal? It's just a single bit of information!"
(By the way, if anyone knows how to properly embed a laugh track in an html file, please let me know.)
So, my point is that the way we measure uncertainty should depend on how we need to use that information. Different decision problems will correspond to different uncertainty measures.
As a sidenote, you may be wondering what decision problem would correspond to Shannon entropy. Read up a little bit on proper scoring rules and I'm sure you can figure it out!
On Conditional Entropy and Families of Functions
I said earlier that I prefer defining the conditional entropy $F(Y|X)$ as the expectation, over a draw from $X$, of the remaining entropy in $Y$. The reason is that this matches perfectly with the definition of the value of $X$ in predicting $Y$, which I wrote as $G(Y|X)$.
The other definition could be $F(X,Y) - F(Y)$. This has no clear analogue in a decision problem because the relevant event of nature, such as $Y$ is fixed. So while $G(Y)$ and $G(Y|X)$ are well-defined from a given decision problem, $G(X,Y)$ is not.
This touches on a subtlety of entropy functions: They are often conflated with a family of entropy functions: one for each possible support size. This is necessary to use notation like $F(X,Y)$ and $F(Y)$ in the same sentence. Unfortunately, there does not seem to be an immediate analogue for decision problems, which are only defined with respect to a particular random event of nature.
But most proper scoring rules, for instance, actually are defined for all support sizes. So for cases like these, and perhaps other families of decision problems, one can compare more easily and direct to their entropic counterparts and ask whether quantities like $F(X,Y) - F(Y)$ are relevant to the decision problems.
More Axioms, More...
An interesting question is to describe further "nice" entropy axioms, and also to investigate how they constrain the corresponding decision problems. To me, the most natural is the following:
- $F$ is symmetric under permutation of a probability distribution (e.g. swapping the probability assigned to two outcomes).
Proposition 4. Axioms B1 and B2 imply that entropy is maximized by the uniform distribution.
Proof. By symmetry, $F$ has the same value at some point $p$ as on each $\sigma(p)$ for any permutation $\sigma$. By concavity, $F$ must be at least as large at the average of all of these points, which is the uniform distribution.
Note that it would probably be good to amend B1 to require strict inequality when $X$ and $Y$ are not independent; in other words, to require $F$ to be strictly concave. One implication would be that the uniform distribution uniquely attains the maximum entropy.
In particular, I think this is the most natural question (please let me know if you are aware of any related work!):
Open Problem/Challenge. Investigate the class of generalized entropies satisfying B1 and either of the following two axioms:
- $F(X) + F(Y|X) \leq F(X,Y)$.
- $F(X) + F(Y|X) \geq F(X,Y)$.
It may help to interpret this question in terms of conditional prediction problems. (Some background on proper scoring rules is useful here.) An agent is asked to make a prediction in two different ways (one for each side of the inequality). In one scenario, the agent is asked to predict the joint outcomes of $X$ and $Y$. Her expected score is $G(X,Y)$. In the other scenario, she is asked to predict the outcome of $X$, and also to give a prediction about $Y$ given each possible $x$. She will be scored only for the conditional prediction of the $x$ that occurs; her total expected score here is $G(X) + G(Y|X)$, assuming the same (family of) scoring rule $G$ is used for both cases.
Now, Axiom S3a says that her expected score should be weakly higher in the two-stage prediction scenario; Axiom S3b says that it should be weakly higher in the joint prediction scenario. (Recall the correspondence is $F = - G$.) Only for the $\log$ scoring rule will her score be exactly equal in either case.
Another way to think of S3a and S3b are in terms of source coding. Imagine that we need to send the realization of a pair $(X,Y)$ over a wire. We choose an encoding scheme and pay an average cost $F$ for optimal encoding. (For Shannon entropy, the cost is the number of bits used for the encoding.)
$F(X,Y)$ corresponds to the expected "cost" for optimally encoding and sending the realization of the pair $(X,Y)$ treated as a single random variable. Meanwhile, $F(X) + F(Y|X)$ corresponds to the total "cost" for first encoding the realization of $X$ optimally, then optimally encoding the realization of $Y$ given $X$. So the axioms state whether it is always preferable to encode an entire realization at once, or whether one should encode piece-by-piece.
But despite such interpretations, I don't have an intuition yet for which axiom I should prefer, or even an idea of which is satisfied by common proper scoring rules. Please, investigate and enlighten me!
References
(1948) Claude E. Shannon. A mathematical theory of communication. The Bell System Technical Journal.(1966) Ronald A. Howard. Information value theory. IEEE Transactions on Systems Science and Cybernetics.

