Eliciting Means

Posted: 2018-08-02.

It turns out that Bregman divergences generally characterize scoring rules to elicit an agent's expectation of a random variable. This fact is important in machine learning and also has nice connections to the proper scoring rule characterization. This is a continuation of the series on elicitation.

What Does It All Mean?

Suppose Expert Emma knows the entire probability distribution of some random variable, say, the winning time in the marathon at the next Olympics. But Impatient Ingrid doesn't have time to elicit the entire distribution, which may be complex and require a lot of information to describe. Or maybe Emma would have trouble writing down the exact distribution at every point, but she does have some strong beliefs about it.

Either way, Ingrid wants to just truthfully elicit some concise summary or property of the distribution. So rather than using a proper scoring rule to elicit the full distribution from Emma, she just wants to elicit a property of the distribution. And not just any property: the mean, a.k.a. expectation.

Our goal is to help out Ingrid by characterizing all scoring rules to elicit the mean of a distribution.

Above: a complex, difficult-to-describe-and-report probability density function.

Below: a nice, simple, easy-to-report number (the average of that distribution).

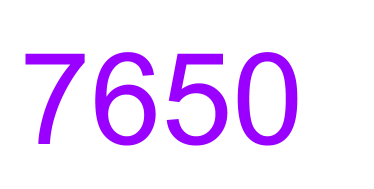
Setup

As in previous posts on elicitation: Emma has a belief $p$ in some set $\mathcal{P}$ of distributions on $Y$, a random variable. Today $Y$ can be vector-valued, so the outcome of the random variable is a point $y \in \mathbb{R}^d$.

Ingrid will use a scoring rule $S: \mathbb{R}^d \times \mathcal{Y}$. It takes a prediction $r$ of the mean of $Y$, along with the actual observed outcome $y$, and returns Emma's score $S(r,y)$. The scoring rule elicits the mean if Emma's optimal report (in the sense of maximizing expected score) is to report her expectation: $$ \Gamma(p) = \arg\max_{r \in \mathbb{R}^d} \mathbb{E}_p S(r, Y) . $$

Key Characterization Idea

Now, we already know the general characterization of scoring rules eliciting any property. It implies that every scoring rule $S$ that elicits the mean corresponds to a convex function $\bar{G}: \Delta_{\mathcal{Y}} \to \mathbb{R}$ whose graph is a pointwise maximum of hyperplanes. Each hyperplane corresponds to a different report $r$ and is tangent to $\bar{G}$ precisely above the beliefs $p \in \Delta_{\mathcal{Y}}$ where $r$ is the mean, i.e. $\mathbb{E}_{y\sim p} y = r$.

The probability simplex on three outcomes: $y=-1$, $y=0$, and $y=1$. So each point in the simplex is a distribution on these three possibilities; a vertical line is a set of distributions all of which have the same mean. For instance, the middle vertical line consists of all beliefs with mean zero.

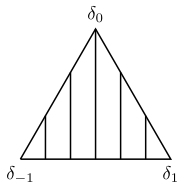
Notice that the level sets in the plot consist of parallel lines; this is always true for a real-valued random variable. In higher dimensions, these are parallel hyperplanes. Now take a pipe and slice it in half lengthwise, ending up with a convex function that snowboarders call a halfpipe. (If you look at it head-on, you see the lower half of a circle.) Hold it horizontally over the simplex so that it lines up with the level sets of the mean: any tangent hyperplane touches the halfpipe directly over one of the parallel lines.

A single convex function of the mean, "stretched" across the simplex in the direction of the level sets.

The key point is that you can raise and lower either end of the halfpipe, or rotate it a bit, and still get the same level sets. But that's all you can do -- in particular, you couldn't twist one end into a non-perfect half circle without changing the level sets. So really there's only a one-dimensional convex function here: the half-circle. And it's a convex function of the mean. You can add any linear function to it (for example, raise or lower the far end or the left side), but that's all you can do while still satisfying the general characterization.

So the characterization for eliciting the mean will state this formally: every scoring rule for the mean can be derived from a convex function of the mean along with some linear shift. Note here a linear shift of the expected score function has a nice interpretation in terms of the scoring rule: It can be written as a "bonus" $f(y)$ given to Expert Emma when $Y=y$. In this case, one' expected score for any belief $q$ is shifted by the linear function $\mathbb{E}_{y\sim q} f(y)$.

Characterization

The results in Abernethy-Frongillo 2012 (see also Banerjee et al. 2005, a more restricted case) produce the following theorem.

The key piece of the proof is arguing the "halfpipe property" that the $\bar{G}$ function of the general characterization really is just a "stretch" of $G$. In other words, the subgradients of $\bar{G}$, in directions parallel to the level sets, are equal; they only differ in directions non-parallel to the level sets.

Now, recall that the Bregman divergence of a convex function $G$ is defined as \[ D_G(y,r) = G(y) - \left[ G(r) + dG(r) \cdot (y - r) \right] . \] Since the above characterization holds for arbitrary $f(y)$, we can let $f(y) = -G(y) + \hat{f}(y)$ for arbitrary $\hat{f}(y)$ and the characterization is still true. This gives the following corollary (exercise: work out the steps on pen and paper if you don't see it immediately!).

Exercise. Show that every proper scoring rule (for eliciting a probability distribution) is a special case, i.e. can be interpreted as a proper scoring rule for eliciting the mean of a random variable.
Hint: compare the characterization of proper scoring rules to the above.

Machine Learning Applications

This time, say Ingrid is interested in data of the form $(x,y)$ where $x$ are "features" and $y$ is an outcome or response variable. For example, perhaps $x$ describes a person's demographics and $y$ is kilograms of chocolate eaten per year. Ingrid wants to understand the high-level relationship between demographics and chocolate consumption, so she asks Emma to provide a hypothesis $h: \mathcal{X} \to \mathcal{Y}$. Given features $x$, $h(x)$ is a prediction for expected kilograms eaten.

In order to elicit a good hypothesis from Emma, Ingrid can measure performance using a loss function $\ell(r, y)$ where $r = h(x)$ is the prediction and $y$ is the true value. In this case, Emma's expected loss (measured over pairs $x,y$ drawn from some population of people) is \[ \mathbb{E}_{x,y} \ell(h(x), y) . \]

What loss function should Ingrid use? Well, if $h(x)$ is supposed to predict the expectation of $y$ given $x$, then for any hope of statistical consistency, the loss $\ell$ should elicit the mean. (It then follows that Emma can minimize expected loss with a hypothesis that always predicts the mean. Under some assumptions on her hypothesis class, she can asymptotically find such a hypothesis by minimizing empirical loss on a large data set, asymptotically -- see Agarwal and Agarwal 2015.)

I say a loss function "elicits the mean" if $\ell(r,y) = -S(r,y)$ for some scoring rule $S$ that elicits the mean, since then by definition, minimizing expected loss corresponds to maximizing expected score which is achieved by the expectation of $y$.

Example/exercise 2: squared loss. Recall from proper scoring rules that the Brier (quadratic) score $S(p,y) = 2p(y) - \|p\|_2^2$ is derived from the convex function $\bar{G}(p) = \|p\|_2^2 = \sum_y p(y)^2$. Similarly, for eliciting the mean, we can start from the convex function $G(x) = \|x\|_2^2 = \sum_j x_j^2$. Show using the characterization theorem or corollary that the mean is elicited by the squared loss $\ell(r,y) = (r-y)^2$.

Linear Properties and Notes

With a bit of notation, we can extend these results. In general, suppose that Ingrid will observe a draw $\omega$ from a sample space $\Omega$, and that a random variable $Y$ can be written as a function $Y: \Omega \to \mathbb{R}^d$. In this case, if Emma has a belief $p \in \Delta_{\Omega}$, then we can think of her expected value of $Y$ as a linear function of her belief $p$, as $\mathbb{E}_p Y = \sum_{\omega} Y(\omega)p(\omega)$. Abernethy and Frongillo (2012) extend the above result to this setting, showing that the Bregman-divergence characterization applies to all such linear properties.

Notes. This kind of result was first proved in the machine learning community by Banerjee et al., possibly unaware of the close connection to Savage's proper scoring rule characterization. I haven't been worrying about the distinction between finite and infinite outcome spaces (whether $Y$ or $\Omega$ take a finite set of possible values) in this post. It turns out that they do generalize, however, and this was explored by Frigyik et al. 2008 and is covered by Abernethy and Frongillo, who extended this result and placed it in the elicitation context.