Convexity
Posted: 2016-09-20.
Convexity is a simple, intuitive, yet surprisingly powerful mathematical concept. It shows up repeatedly in the study of efficient algorithms and in game theory. The goal of this article to is to review the basics so we can put convexity to use later.
Convex sets
In a vector space such as $\mathbb{R}^n$, a set $S$ is convex if, for every two points in $S$, the entire line segment between the points is also in the set.
In notation, $S$ is convex if for all $x,y \in S$ and all $\alpha \in [0,1]$, $\alpha x + (1-\alpha)y \in S$.
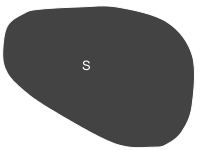
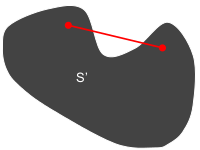
A convex ($S$) and non-convex ($S'$) set.
Most but not all potatoes are convex. Most but not all bananas are non-convex.
Convex sets don't have to be closed or compact; $\mathbb{R}^n$ itself is a convex set. One important convex set is a halfspace: all points on one side of a hyperplane.
A nice fact is that the intersection of any number of convex sets is convex (can you prove it?). In particular, an intersection of a finite number of halfspaces is called a convex polytope. Examples are cubes and tetrahedra. Convex polytopes are the central object of study in linear programming.
Given a set of points, their convex hull is the smallest convex set containing all the points. The convex hull of a hula hoop is a disk. The convex hull of the set of four points consisting of the corners of a soccer field is the entire soccer field. (Yes, I'm American.) The convex hull of a soccer ball is a soccer ball.
Convex functions
Given a function $G$ from a vector space to scalars, e.g. $G: \mathbb{R}^n \to \mathbb{R}$, its epigraph is the set of points lying above the function.In notation, epi $G = \{(x,y) : y \geq G(x) \}$.
$G$ is a convex function if its epigraph is a convex set.
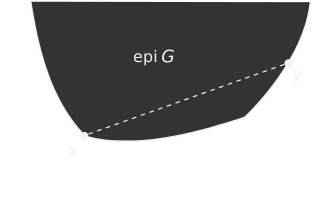
The epigraph of a convex function $G$.
You'd more often see a definition such as: $G$ is convex if, for all $x,x'$ and all $\alpha \in [0,1]$, $G\left(\alpha x + (1-\alpha)x'\right) \geq \alpha G(x) + (1-\alpha)G(x')$. Check the equivalence!
A very nice fact, or perhaps beautiful definition of convexity, is Jensen's inequality: If $G$ is convex, then for any random variable $X$, $\mathbb{E}G(X) \geq G\left(\mathbb{E} X\right)$.
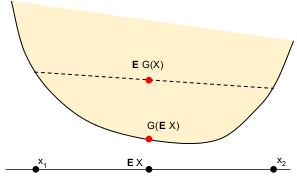
You'll never forget which way Jensen's inequality goes if you keep the picture in mind.
A nice fact is that the pointwise maximum of a set of convex functions is itself a convex function. That is, if $G_i$ is convex for all $i$, then $G(x) = \max_i G_i(x)$ is convex. Exercise: prove it! (Use our definition of convexity and a nice fact from the previous section.)
There are many other nice facts about convex functions (I feel like I'm noticing a pattern). They are continuous on the interior of their domain. If $G_1$ and $G_2$ are convex and $\alpha,\beta \gt 0$, then $\alpha G_1 + \beta G_2$ is convex.
Subgradients and such
A subtangent of $G$ is a linear function that shares at least one point with $G$ and lies everywhere below $G$. If $G$ is convex then it has a subtangent at every point $x$ in its interior. Furthermore, this subtangent can be written $f(x') = G(x) + \langle r, x' - x \rangle$ for some vector $r$.
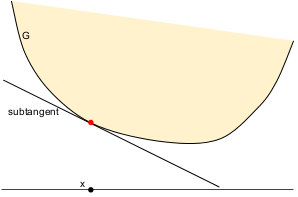
A subtangent is a linear approximation to $G$ at $x$.
The vector $r$ in the above definition is a subgradient of $G$ at $x$. In other words, $G(x') \geq G(x) + \langle r, x' - x\rangle$ for all $x'$.
If $G$ is differentiable at $x$, then there is only one subgradient at $x$, which is the derivative at $x$. You can consider $G(x) = |x|$ at $x=0$ to see the converse; there are many possible subtangents at that point.
Because it only helps intuition to think of the subgradient as a generalization of the derivative, I like to use the notation $dG_x$ for a subgradient of $G$ at $x$.
Bregman divergences
This function is simply a measure of how far a subtangent is below $G$. The Bregman divergence of $G$ is \[ D_G(x,y) = G(x) - \Big[ G(y) + \langle dG_y, x-y \rangle \Big] . \]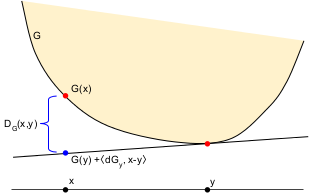
It's easy to remember the order of the arguments: $D_G(x,y)$ is always at least zero because it's $G(x)$ (the first argument) minus the linear approximation at $y$ (the second argument).
Don't memorize the formula; memorize the figure and reconstruct the formula!
Bregman divergence is often considered a sort of distance measure (though not technically a metric), because it is nonnegative and equals zero if $x = y$. This is an only if when $G$ is strictly convex, meaning that no subtangent intersects $G$ at more than one point.
Example/exercise 1.
Consider the convex function on $\mathbb{R}^n$ defined by $x \mapsto \|x\|_2^2 = \sum_i x_i^2$.
Show that its Bregman divergence is just $\|x-y\|_2^2$. Conclude that its Bregman divergence is a distance metric.
Example/exercise 2.
If we let $p$ be a probability distribution on a finite domain, then the function $p \mapsto \sum_i p_i \log(p_i)$ is convex (it is the negative of the Shannon entropy function).
Show that the Bregman divergence of this function is the relative entropy (also called KL-divergence) $KL(p,q) = \sum_i p_i \log\frac{p_i}{q_i}$.
Problem.
Show that $\|x-y\|_2^2$ is the unique symmetric Bregman divergence (hence the only Bregman divergence that is also a distance metric).

