Hybrid Auction-Prediction Mechanisms
Posted: 2018-06-23.
This post describes a mechanism for making a group decision (along with monetary transfers) based both on people's preferences and their predictions.
This mechanism was proposed in 2013 by myself, Yang Cai, Mohammad Mahdian, and Aranyak Mehta; however, this post contains some additional thoughts of my own on applications of this mechanism.
Examples
Let's start with some potentially motivating examples.
- Auctions. Our city wants to choose a contractor to build a bridge. Each contractor knows their own cost for construction, and also the probability that a bridge they build will fall down in the next ten years. Rather than just assigning the contract to the lowest bidder, we want to optimize a combination of cheap costs and reliability (without contractors lying about either).
- Combinatorial mechanism design. I want to purchase access to a route through a network, from $s$ to $t$. Each edge will "bid" their cost for me to utilize that edge, and a probability distribution over the length of travel time. I want to optimize a tradeoff between total travel time and total cost, and I don't want edges lying to me about delay distributions in order to get my business.
- Public projects; elections. Our city wants to build either a tennis court or a swimming pool. We have a metric, e.g. total number of users of the new facility in its first year. Each citizen submits a bid (describing their value for each project) and a probability distribution over how many times they would use each facility in the first year. We pick the project that maximizes some combination of total "value" according to the bids and total expected usage, without giving citizens incentives to exaggerate their expected usage.
The common thread is that people have both preferences and predictions. We want a mechanism to aggregate them both to make a decision. We want to make it dominant-strategy truthful (a best response is always to report truthfully) and will use monetary transfers. Crucially, we will get to wait and see the outcome of the event (whether the bridge falls, how long the travel takes, how many times the citizen uses the facility) and we can reward accurate predictions.
Model
The setting and mechanism will be based on the VCG mechanism, knowledge of which is a helpful prerequisite. It will also be helpful to know about proper scoring rules, since the main idea here is to squish together VCG and scoring rules into a single mechanism. (But to get truthfulness, we have to integrate the two carefully -- it won't work to just apply them each separately!)
There is a set $A$ of alternatives (the set of contractors; the set of all $s \to t$ routes; the set $\{\text{tennis court}, \text{pool}\}$). There are bidders $1,\dots,n$ (the contractors; the edges of the network; the citizens). There is also an observable future event whose outcome will be in the set $\Omega$. This could be the set $\{\text{bridge falls down}, \text{bridge stays up}\}$; or the set $\mathbb{R}$ of all possible lengths of travel time; or the set $\{0,1,2,3,\dots\}$ of possible number of times the facility is used by that citizen.
Each bidder $i$ has a valuation function $v_i: A \to \mathbb{R}$, and a set of conditional beliefs $\{p_i^a : a \in A\}$. Here $v_i(a)$ is the valuation or gain in utility to the bidder if alternative $a$ is selected. $p_i^a$ is an element of $\Delta_{\Omega}$, that is, a probability distribution over the future event's outcomes. It represents the agent's belief conditioned on selecting alternative $a$. (For example, if $a = $ tennis court, then $p_i^a$ is my distribution over how many times I will use the tennis court, and if $a' = $ pool, then $p_i^{a'}$ is my distribution over how many times I will use the pool. Write $p_i$ as shorthand for this entire set of conditional beliefs.
Objective
First, say that for each alternative $a$, we have an "aggregation function" $g_a(p_1^a,\dots,p_n^a)$. The function $g_a$ takes in all the predictions from all the bidders and outputs a sort of social value assigned to selecting alternative $a$ when the $n$ agents' predictions are $p_1^a \dots p_n^a$. Okay, then our objective is to pick the alternative maximizing social welfare, including this external social value:
$$ W(a) = \arg\max_{a\in A} ~~ \left(\sum_{i=1}^n v_i(a)\right) + g_a(p_1^a,\dots,p_n^a) $$We also require that $g_a$ should be well-defined if it only gets $n-1$ inputs, i.e. if we omit any one bidder's predictions $p_i$. Our algorithm should do the following:
- Take as input $(v_1,p_1), \dots, (v_n,p_n)$.
- Output the alternative $a^*$ maximizing $W(a)$.
- Also output, for each bidder $i$, a conditional payment function $\pi_i^{a^*}: \Omega \to \mathbb{R}$.
- Later, when the outcome $\omega$ of the event is observed, the bidder pays $\pi_i^{a^*}(\omega)$.
The question is how to choose payment functions for dominant-strategy truthfulness: regardless of all other agents' actions, each bidder's optimal strategy is to report both $v_i$ and $p_i$ truthfully (all conditional predictions). We assume the bidders want to maximize expected utility:
$$ v_i(a) - \mathbb{E} \pi_i^a(\omega) $$ where the expectation is over $\omega$ being drawn according to $p_i^a$; remember, this is what $i$ believes is the distribution of $\omega$ conditioned on alternative $a$.Mechanism
There are two key ideas to the mechanism. First, we use VCG-style payments, but with this modified objective $W(a)$ that includes the $g_a$ function.
Second, we assume that $g_a$ is convex in each $p_i^a$ when we fix the reports of all $j\neq i$. So we know from the theory of proper scoring rules that we can decompose $g_a$ into a proper scoring rule $S_a(p_i^a, \omega)$ such that expected score for belief $p_i^a$ is at most $g_a(\dots,p_i^a,\dots)$, with equality if reporting truthfully. So in the VCG-style payment rule, when we are supposed to pay the agent $g_a$, we instead pay them a proper scoring rule. Their expected score is still $g_a$ if truthful (so the rest of the VCG argument still works), and only less if they lie.Notation:
- $W(a) = \left(\sum_{i=1}^n v_i(a) \right) + g_a(p_1^a,\dots,p_n^a)$, the "welfare" of $a$.
- $a^* = \arg\max_a W(a)$, the welfare-maximizing alternative.
- $p_{-i}^a = $ the vector of predictions $p_1^a,\dots,p_n^a$ but with $p_i^a$ removed.
- $W_{-i}(a) = \left(\sum_{j\neq i} v_j(a) \right) + g_a(p_{-i}^a)$, the welfare if $i$ doesn't arrive.
- $a_{-i}^* = \arg\max_a W_{-i}(a)$, the optimal alternative if $i$ doesn't arrive.
Fixing all others' reports $p_{-i}^a$, the proper scoring rule characterization says that there is a scoring rule $S_i^a$, where $S_i^a(p_i^a, \omega)$ is the score for reporting $p_i^a$ when the observed outcome is $\omega$, satisfying the following properties:
- $S_i^a$ is proper, meaning that the expected score is maximized by reporting one's true belief $p_i^a$ about the event.
- For any belief $p_i^a$, the expected score for all reports is at most $g_a(p_{-i}^a, p_i^a)$, with equality if $i$ reports $p_i^a$ truthfully.
Theorem. Suppose that each $g_a$ is component-wise convex, i.e. for each $i$, $g_a$ is convex in the argument $p_i^a$. Then there is a dominant-strategy truthful mechanism to maximize $W(a)$, with payment rule: $$ \pi_i^a(\omega) = W_{-i}(a_{-i}^*) - \sum_{j\neq i} v_j(a) - S_i^a(p_i^a, \omega) . $$
Proof.
Fixing all others' reports, $i$'s utility for any outcome $a$ being selected when she is reporting $\hat{p}_i$ (which may be a lie) is \begin{align*} \text{utility} &= v_i(a) - \mathbb{E} \pi_i^a(\omega) \\ &= v_i(a) + \sum_{j\neq i} v_j(a) + \mathbb{E} S_i^a(\hat{p}_i^a, \omega) - W_{-i}(a_{-i}^*) \\ &= \sum_{j=1}^n v_j(a) + \mathbb{E} S_i^a(\hat{p}_i^a, \omega) - W_{-i}(a_{-i}^*) \end{align*} Now, for any alternative $a$, by definition of properness of the scoring rule $S_i^a$, we have $\mathbb{E} S_i^a(\hat{p}_i^a, \omega) \leq \mathbb{E} S_i^a(p_i^a, \omega) = g_a(p_1^a,\dots,p_n^a)$. So \begin{align*} \text{utility} &\leq \sum_{j=1}^n v_j(a) + g_a(p_1^a,\dots,p_n^a) - W_{-i}(a_{-i}^*) \\ &= W(a) - W_{-i}(a_{-i}^*) \\ &\leq W(a^*) - W_{-i}(a_{-i}^*) . \end{align*} The last $\leq$ is justified by the definition of $a^*$ as the optimal alternative. But this is exactly $i$'s expected utility if she reports everything truthfully! (If she is truthful, the mechanism picks $a^*$, and her expected score is $g_{a^*}$.) So she maximizes expected utility by truthfulness.Examples continued
Let's see how this vague theory could play out in the examples described above.
Auctions. Each contractor is a bidder $i$ with a valuation $v_i(a) = w_i$ if $a=i$ so that they win the contract, and $v_i(a) = 0$ otherwise. Here $w_i$ is some positive number. Here the set of observable outcomes of the event is $\Omega = \{\text{falls down}, \text{stays up}\}$. They also have a probability $q_i \in [0,1]$ for the probability that their bridge stays up, so if $a=i$, then $p_i^a(\text{fall down}) = 1-q_i$ and $p_i^a(\text{stay up}) = q_i$, and they don't need to report any beliefs about $a \neq i$.
How should we measure "external welfare" $g_a(p_1,\dots,p_n)$ as a function of the reported probabilities? It should only depend on the winning bidder $a$'s predicted probability that her own bridge stays up. So we can have e.g. for each $a=i$ then $g_a(p_1,\dots,p_n) = 2^{20q_i}$. In other words, the social utility for the bridge definitely falling down is $2^{10(0)} = 1$, and the utility for it definitely staying up is $2^{20(1)} \approx 1$ million, and the utility for e.g. it having a $0.5$ chance of staying up is $2^{20(0.5)} \approx 1000$.
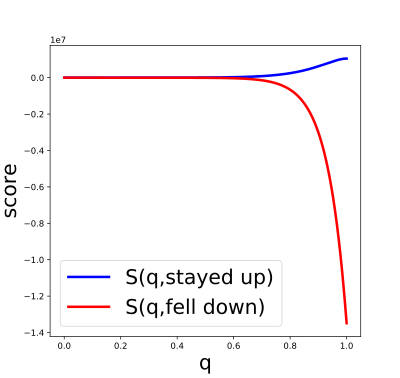
Now this is a generalization of the second-price auction. The winner is the bidder $i$ that maximizes $w_i + 2^{20q_i}$. Let $j$ be the "second-highest" bidder, i.e. has the second-largest $w_j + 2^{20q_j}$. The standard Groves approach would charge the winner $$ w_j + 2^{20q_j} - 2^{20q_i} $$ but of course this would not be truthful for $i$ in reporting $q_i$. Instead, we charge them $$ w_j + 2^{20q_j} - S(q_i, \omega) $$ where $\omega$ is either "falls down" or "stays up" (of course, we have to wait 10 years to observe this). For the convex function $2^{20q_i}$, the proper scoring rule is: $$ S(q_i, \omega) = \begin{cases} 2^{20q_i} + (20\ln(2))2^{20q_i}\left(1 - q_i\right) & \text{stayed up} \\ 2^{20q_i} - (20\ln(2))2^{20q_i} q_i & \text{fell down} \end{cases} $$ In other words, this looks like the contractor agreeing to receive a certain bonus after 10 years if the bridge is still up, or pay out a big penalty if it has fallen down. The larger their prediction $q_i$, the larger these penalties/bonuses (see the figure).
Below: for each outcome, the score $S$ as a function of prediction $q$, where $S$ is the proper scoring rule derived from the convex function $2^{20q}$. Notice the vertical axis is in units of tens of millions.
Combinatorial mechanisms. In the "buying a route" example, each edge in the graph is a bidder $i$ who has a valuation $v_i(a) = -c_i$ if the route $a$ passes through edge $i$, and $v_i(a) = 0$ otherwise. Here $c_i$ is the cost to that edge of routing traffic. Meanwhile (and this is a slight extension of the model as described above), $i$ knows the distribution $q_i$ over delay times on her edge. For instance, maybe all delays are integers between $0$ and $100$, plus the possibility of failure of the edge to successfully route the traffic, so $q_i$ is a distribution over these $102$ possibilities. If the route $a$ does not include edge $i$, then $i$ doesn't need to have any beliefs or make any predictions.
How do we pick $g$ for this application? It should be a function of the probabilities of all edges $i$ in the route $a$. One possibility is simply the overall probability of successful routing, which is $$ f_a(q_1,\dots,q_n) = \prod_{i \in a} \left(1 - q_i(\text{failure on edge $i$})\right) $$ This is convex in each $q_i$ when we fix all the others. However, it would be nicer to use a strictly convex function which better incentivizes truthfulness of $q_i$ (with a linear function, agents may misreport in a way that doesn't change your decision). Another possibility, if there are no failures, is some convex function of expected travel time. If my maximum total travel time is $1000$, I could choose $$ h_a(q_1,\dots,q_n) = \left(1000 - \sum_{i \in a} \mathbb{E} \left[ \text{travel time $\leftarrow q_i$}\right]\right)^2 $$ Maybe most reasonable is some combination of $f_a$, which measures my utility for routes with different probabilities of success versus failure, and some choice of $h_a$, which measures my utility for different routes with different expected travel times. So we would have $$ g_a(q_1,\dots,q_n) = f_a(q_1,\dots,q_n) + h_a(q_1,\dots,q_n) $$
Now the auction looks more complicated, but is not computationally difficult. In practice, it would probably be helpful to show bidders plots of the scoring rule used (as above) so they can understand their risk.
Public projects; elections. Let's say we want to decide whether to impose a new tax or not, and the metric we care about is GDP in two years. Each bidder preferences expressed as $v_i(\text{tax}), v_i(\text{not})$. They also have a belief as probability distributions $p_i^{\text{tax}}, p_i^{\text{not}}$ over GDP conditioned on passing the tax or not.
Designing $g_{\text{tax}}, g_{\text{not}}$ is very interesting in this context. One natural first choice would be to first aggregate the predictions for each $a$ into a single distribution on GDP, and measure utility as proportional to expected GDP. If our aggregation is just the average of the $p_i^a$, this is linear in each $p_i^a$ and therefore (weakly) convex: $$ g_a(p_1^a,\dots,p_n^a) = \frac{1}{n} \sum_{i=1}^n \mathbb{E} \left[\text{GDP $\leftarrow p_i^a$}\right] $$ As mentioned above, it might be preferable to have a strictly convex $g_a$, and the right choice is a great question for further investigation.
The mechanism would choose $a = $ tax or $a = $ not depending on which maximizes $$ \left(\sum_{i=1}^n v_i(a)\right) + g_a(p_1^a,\dots,p_n^a) $$ The payments would look like this. If $i$'s presence doesn't change the outcome (say we impose the tax, and we would have done so even if $i$ didn't show up), then $i$ is paid by a proper scoring rule, minus some constant. If $S_{tax}$ is the proper scoring rule corresponding to $g_{tax}$ when we fix $p_{-i}^{tax}$, then $i$ is paid by the mechanism (or pays, if negative): $$ S_{tax}(p_i^{tax}, \text{observed GDP}) - g_{tax}(p_{-i}^{tax}) $$ If $i$'s presence does change the outcome (say it flips from not imposing to imposing), then $i$'s payment looks like a combination of the standard VCG payment with a proper scoring rule: $$ W_{-i}(\text{not}) - g_{not}(p_{-i}^{not}) - W_{-i}(\text{tax}) - S_{tax}(p_i^{tax}, \text{observed GDP}) . $$
About g
The function $g$ plays several interesting roles in this mechanism. A first comment is that we cannot loosen the assumption that $g$ is component-wise convex and still get a truthful mechanism. This is part of a larger characterization due to Frongillo and Kash (2014). Now, let's dig a bit further into the role of $g$ and what convexity means for applications.
$g$ plays two roles:
- It aggregates information, collecting everyone's predictions into a decision (which is also based on the valuations, of course).
- It estimates welfare given a set of predictions. We can think of $g_a(p_1^a,\dots,p_n^a)$ as measuring the welfare impact on the rest of the world outside the set of bidders. Hence the objective $$ \left(\sum_{i=1}^n v_i(a) \right) + g_a(p_1^a,\dots,p_n^a) $$ really does measure "social welfare" (under our assumptions), since it is the sum of the bidders' valuations plus the welfare of everyone else in the world. (For example, the auctioneer can put her own utility into the objective by building it into $g$.) Also, by scaling $g_a$ up or down (say multiplying it by 1mill), we can elevate or decrease its importance relative to the bids $v_i$ in determining the final decision.
Convexity and risk aversion. In many cases, we can think of convexity of $g$ as corresponding to some form of risk aversion. Consider the bridge example; if $q$ is the probability of staying up, perhaps I choose $g_a(q) = 2^{20q}$, a very convex function. This says my utility for a bridge that definitely stays up is $2^{20}$, or about a million; my utility for a bridge that definitely falls down is $2^{20(0)} = 1$; but my utility for a bridge that stays up half the time is not halfway between at 500,000. Instead, it is $2^{20(0.5)} = 2^{10} \approx 1000$. This makes sense: A bridge with a 50% chance of falling down is not nearly half as useful as a perfectly reliable bridge (in fact, probably not useful at all.) More generally, a convex function of probability distributions generally expresses risk aversion because uncertainty is penalized relative to the average value of certainty.
Governance
This mechanism can be viewed as decisionmaking based both on the preferences and beliefs of a population, so it may have some relevance to incentive-aware mechanisms for governance. It may be a bad mechanism for high-stakes public decisionmaking due to budget imbalances in the population (rich voters have outsized influence, quasilinearity fails, etc), and/or it may be repugnant in those settings. But perhaps it has some relevance to low-stakes decisionmaking at a company, private group, community such as a blockchain, etc.
One point of comparison is Robin Hanson's futarchy, which bases governance on decision markets: Voters select the important metrics they want to optimize for, then prediction markets are run to predict the performance on these metrics conditioned on taking each decision. The decision is selected according to which has the most optimistic predictions; trades in all other markets are cancelled and only trades in that market eventually pay out.
The incentive problem with futarchy (ignoring any other problems) is that participants with extremely strong preferences for one decision would prefer to manipulate the markets, making intentionally poor predictions and suffering prediction penalties later. This can only be prevented by others with equally large budgets, who are very confident in their predictions and very comfortable with risk, to trade against the manipulator. Even in the absence of strong preferences over outcomes, incentives to manipulate can be present unless we occasionally threaten to (and do) take suboptimal decisions, just to verify predictions in those markets (see Chen et al. 2011).
In contrast, the mechanism described here is truthful (in theory) by allowing bidders to not only submit predictions, but also bid directly on the governance action in an auction-like format. In this sense, it is perhaps a hybrid of Hanson's futarchy and the system we effectively have today. (To clarify, that was meant to be funny. Not necessarily a joke, but funny.)
A downside of this mechanism even in theory is that it is unlikely to efficiently or correctly aggregate the information contained in predictions. Prediction markets are much better at aggregation because they allow dynamic updating, placing of bets of various sizes, and so on. Here, we simply have a sort of wagering mechanism where everyone submits a single prediction once, without much way to distinguish well-informed forecasters. (Both this mechanism and prediction markets must wait years to see the outcome and reward predictions, another downside of both.)
References
(2011) Yiling Chen, Ian Kash, Michael Ruberry, and Victor Shnayder. Decision markets with good incentives. Proceedings of the 7th Workshop on Internet and Network Economics.(2013) Yang Cai, Mohammad Mahdian, Aranyak Mehta, and Bo Waggoner. Designing markets for daily deals. Proceedings of the 9th Conference on Web and Internet Economics.

