Proper Scoring Rules
Posted: 2016-09-22. Updated: 2018-08-01.
How can we elicit truthful predictions from strategic agents? Proper scoring rules give a surprisingly complete and mathematically beautiful answer. In this post, we'll work up to the classic characterization of all "proper" (truthful) scoring rules in terms of convex functions of probability distributions.
I'll be relying heavily on the primer on convexity. Readers of this page may also enjoy the Information Elicitation page.
Which Way Is the Wind Blowing?
In 1950, Glenn Brier observed that that then-standard methods for evaluating weather forecasts provided bad incentives. Suppose that, every time an expert makes a prediction, we wait until the event occurs and then assign her a score. The expert wants to maximize her score. What's a good choice of "scoring rule"?
Formally, say that the event to be predicted will have an outcome in the set $\mathcal{O}$. These outcomes had better be mutually exclusive (only one will occur) and exhaustive (they cover all possibilities). The so-called expert will provide a probability distribution $p$ over $\mathcal{O}$. For instance, my weather station has assured me there is only a 10% chance of rain tomorrow and a 90% chance of no rain.
Then, we observe the true outcome of the event -- some $o \in \mathcal{O}$ -- and pay the expert $S(p, o)$. This $S$ is a scoring rule: it assigns a score to every prediction on every outcome.
A scoring rule is now called (strictly) proper if, whenever the expert's true belief about the event is $q$, she (uniquely) maximizes her expected score by reporting $p=q$. In other words, she tells us what she really thinks, rather than e.g. what she thinks we want to hear.
Example. The Brier or quadratic scoring rule is \[ S(p,o) = 2p_o - \sum_{o' \in \mathcal{O}} p_{o'}^2 \] where $p_o$ is the probability that $p$ assigns to $o$ and so on.
The second term can be written more concisely as $\|p\|_2^2$, the square of the $\ell_2$ norm of $p$. So this rule can be interpreted as "pay twice the probability assigned to the actual outcome, but then penalize by a 'regularization' term depending on $p$."
To see that the quadratic scoring rule is strictly proper, first compute the expected score for reporting $p$ with belief $q$: \begin{align} \sum_{o \in \mathcal{O}} q_o \left[ 2p_o - \|p\|_2^2 \right] = 2\langle p, q \rangle - \|p\|_2^2 . \end{align} Now, we can confirm that the best report $p$ is to set $p=q$. For example we can take the derivative with respect to any $p_o$ and get $2q_o - 2p_o$, using this to check that $p_0 = q_0$ is the optimal choice.
Example. The log scoring rule, which can be found as far back as Good (1952), is \[ S(p,o) = \log p_o . \]
Example/exercise 1. Prove that it is strictly proper.
What Did You Expect?
Let's introduce some incredibly useful notation: define \[ S(p;q) = \mathbb{E}_{o\sim q} S(p,o) . \] $S(p;q)$ is the expected score, under true belief $q$, for reporting $p$.
In particular, what if your true belief is $\delta_o$, meaning that $o$ will occur with probability one? Then naturally we have $S(p;\delta_o) = S(p,o)$. That is, you know that prediction $p$ will result in payment $S(p,o)$.
And naturally, $S(p;q)$ is a linear function of $q$ (it's an expectation!).
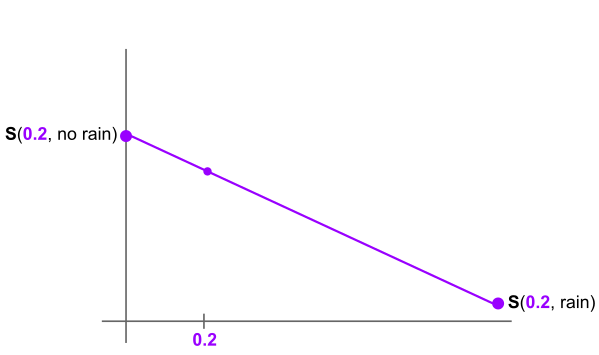
Here the vertical axis is expected score and the horizontal axis is believed probability of rain. On the right at belief $q=1$ we have $S(p;\delta_{\text{rain}}) = S(p, \text{rain})$. The left is analogous. $S(p;\cdot)$ is a linear function between them, since $S(p;q) = q S(p, \text{rain}) + (1-q) S(p, \text{no rain})$.
The Characterization
So we now know that there's one proper scoring rule (the quadratic). And actually, we know that there are two (the logarithmic). By process of induction, our next step is to characterize all of them.
Here's the key question. Given $S$, what can we say about the following "expected score" function? \[ G(q) = S(q ; q) \] $G(q)$ is of course the score for reporting $q$ when $q$ is one's true belief.
Well, first, we already know that $S(p ; \cdot)$ is linear. We also know that $S(p;q) \leq S(q;q) = G(q)$. Why? It's the definition of properness of the scoring rule!
In other words, the line traced by $S(p; \cdot)$ is everywhere below $G(q)$.
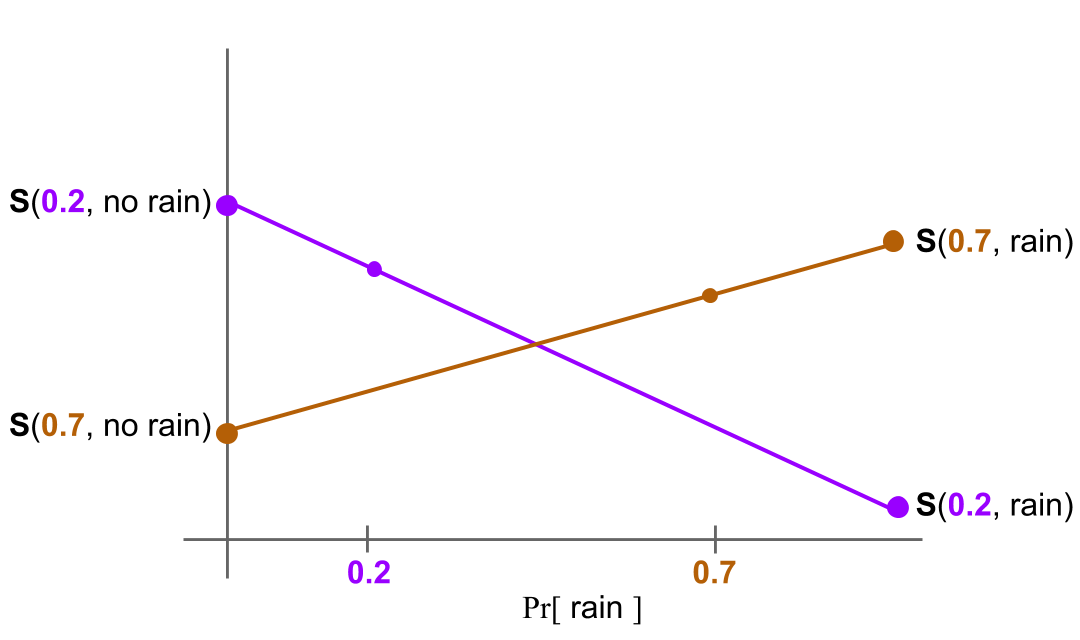
Here are the "expected score lines" for two different reports $p=0.2$ and $p=0.7$.
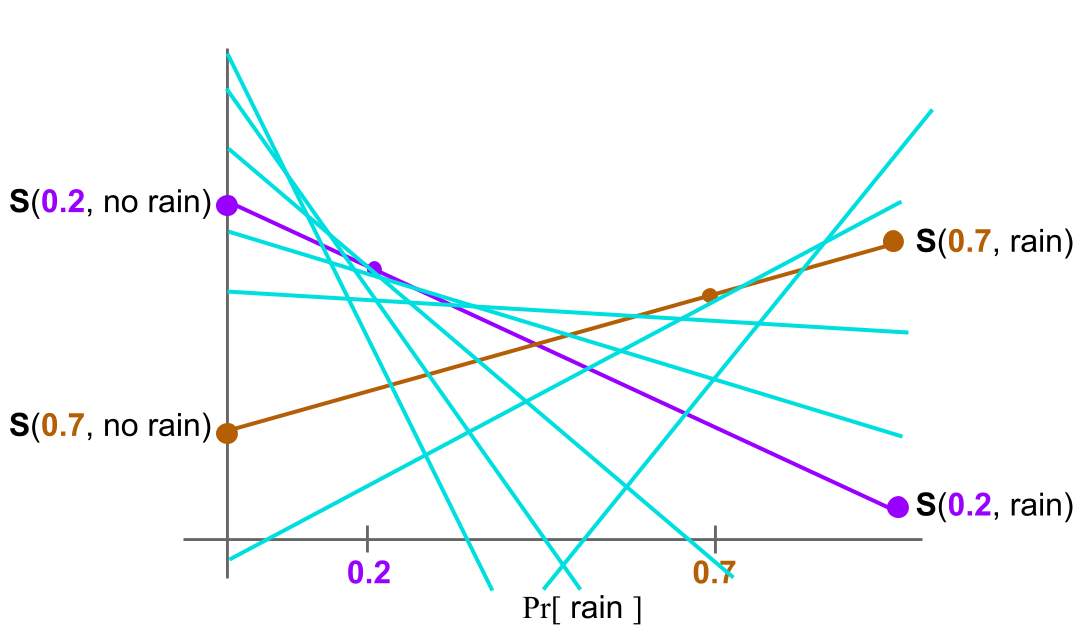
Here are more. We know that, if $S$ is proper, than all of these lines lie below $G$.
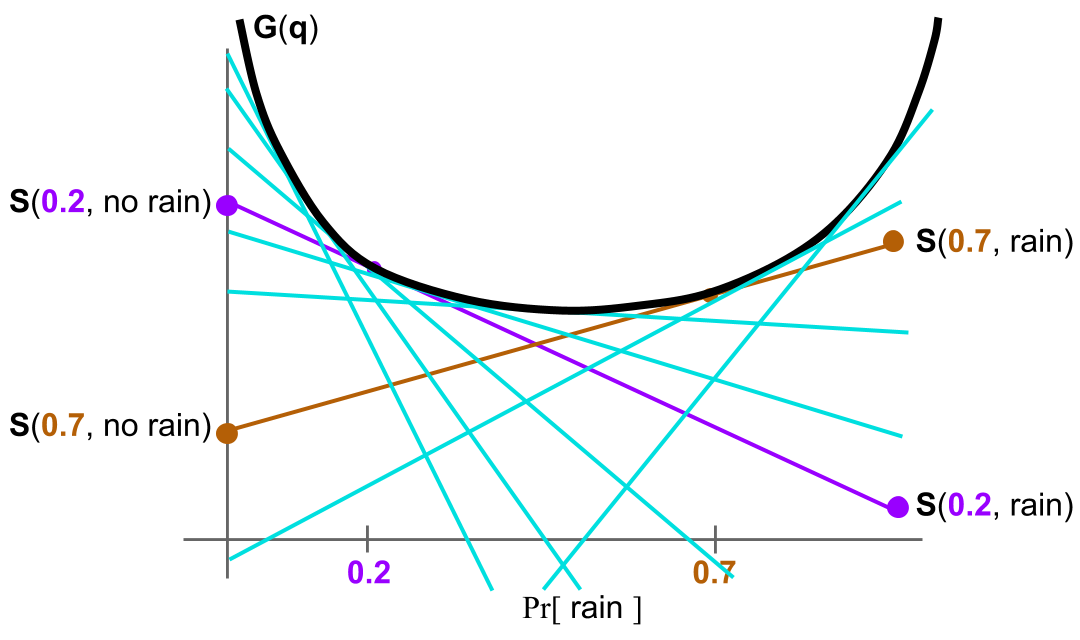
Further, each $S(p;q)$ is tangent to $G$ at $q=p$.
Furthermore, by definition, $S(p; \cdot)$ is equal to $G(q)$ at $p=q$. In other words, $S(p; \cdot)$ is touching (tangent to) $G$ at $q$. This argument, once slightly rigorized, proves the following direction of the scoring rule characterization, which dates back to McCarthy 1956 and Savage 1971.
Theorem. For every proper scoring rule $S(p,o)$, there is a convex "expected truthful score" function $G(q)$ such that $S(q;q) = G(q)$. $S(p; \cdot)$ is a subtangent of $G$, i.e. \[ S(p; q) = G(p) + \langle dG_p, q-p \rangle \] where $dG_p$ is a subgradient of $G$ at $p$. In particular, the scoring rule $S$ can be written \[ S(p, o) = G(p) + \langle dG_p, \delta_o - p \rangle . \]
The reverse direction is easy:
Theorem. For every convex function $G: \Delta_{\mathcal{O}} \to \mathbb{R}$, one can construct a proper scoring rule $S$ by setting \[ S(p, o) := G(p) + \langle dG_p, \delta_o - p \rangle . \]
Proof. Given $G$, let $S$ be defined as above. Because the inner product is linear, we know $S(p;q) = G(p) + \langle dG_p, q - p \rangle$. Now $S(p;q) \leq G(q)$ by the definition of a subgradient. But this is to say $S(p;q) \leq S(q;q)$, which is properness.
So what do we have? The proper scoring rules are in exact correspondence with the convex functions on spaces of probability distributions. (We've focused on finite outcome spaces here, but this can be extended.) The convex function traces out the expected score for being truthful. Given that function, we know how to construct the scoring rule.
Example/exercise 2. Show that both directions of the characterization hold when replacing "proper" by "strictly proper" and "convex" by "strictly convex".
Example/exercise 3. Show that when $S$ is the quadratic scoring rule, $G(q) = \|q\|_2^2$, i.e. $G(q) = \sum_o q_o^2$.
Example/exercise 4. Show that when $S$ is the log scoring rule, $G(q) = -H(q)$ where $H$ is the Shannon entropy.
Further Notes
- This characterization is amazing! It offers a world of proper scoring rules at your fingertips, designed via friendly and tractable convex functions.
- It raises the question of how to pick the right convex function / scoring rule for your application, which I will hopefully have a lot to say about in the future.
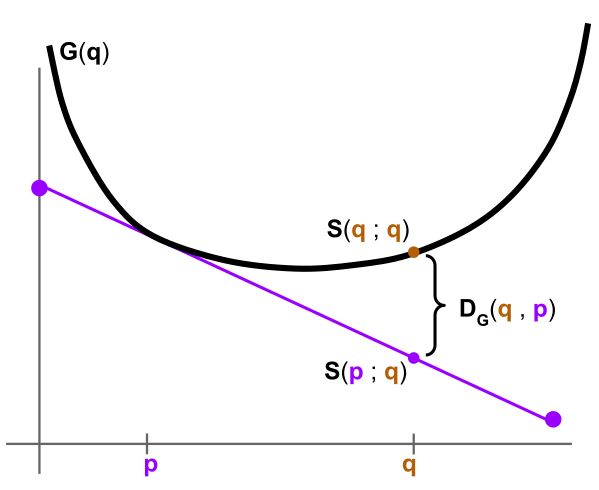
- Recall the Bregman divergence $D_G(q,p)$ of a convex function $G$ is defined to be the difference between $G(q)$ and $G$'s linear approximation at $p$, evaluated at $q$. So another way to define $D_G(q,p)$ is as follows: "Construct the proper scoring rule $S$ from $G$; then output the difference in expected score, under belief $q$, between truthfully reporting and misreporting $p$."
- See the exercises and problems for more "notes".
Example/exercise 5.
Given a strictly proper scoring rule for two outcomes, how could you use it to construct a strictly proper scoring rule on $n$ outcomes?
What would be the relationship of the expected score functions?
Exercise 1. (scalars versus vectors)
Consider the convex function of a single variable $G(p) = p^2$.
Suppose there are two outcomes and interpret $p$ as probability of the first outcome.
Construct a proper scoring rule $S$ for two outcomes corresponding to $G$.
How do $S$ and $G$ differ from the quadratic scoring rule?
Problem 1.
Suppose we want our proper scoring rule to be decomposable in the sense that $S(p,o)$ depends only on $p_o$ and not on the rest of $p$.
Prove that the only proper scoring rule with this property is the log scoring rule.
References
(1950) Glenn W. Brier. Verification of forecasts expressed in terms of probability. Monthly Weather Review.(1952) Irving J. Good. Rational decisions. Journal of the Royal Statistical Society.
(1956) John McCarthy. Measures of the value of information. Proceedings of the National Academy of Sciences.
(1971) Leonard J. Savage. Elicitation of personal probabilities and expectations. Journal of the American Statistical Association.
(2007) Tilman Gneiting and Adrian E. Raftery. Strictly proper scoring rules, prediction, and estimation. Journal of the American Statistical Association.


Comments
Since I have been blocked by A. R. Pruss from his blog, I wonder, what do you think about his intuitions about strictly proper scoring rules.
He made a reference for this post of yours in this recent post of his about strictly proper scoring rules: "Open-mindedness and propriety" by A. R. Pruss (Wednesday, February 1, 2023: https://alexanderpruss.blogspot.com/2023/02/open-mindedness-and-propriety.html )
How is that man considered to be a "mathematician" by so many?!?
Siriously, HOW?!?
Best regards,
Zsolt Nagy