Fairness in Machine Learning: A Biased Primer

Posted: 2019-02-23.

This post will summarize some of the motivation for and definitions of fairness in ML. This is a huge and evolving topic -- here we'll focus a bit on discrimination in algorithmic decisionmaking. We'll spend relatively less time on motivations and real-world examples, more at the highest and lowest-level meanings of fair machine learning.

Note - throughout the post, I'll try to use a variety of fairness examples such as gender and racial bias. But the goal is not to solve these problems today, but instead to think through examples at an abstract level and provoke further thought. None of the examples should be interpreted or construed as my having any opinions, beliefs, or thoughts whatsoever about anything.

0. From the beginning

In today's world and the foreseeable future, algorithms are involved in decisions affecting people's lives. This includes what "content" (or advertisements) to show or recommend on the Internet, but also things like loan and job applications and prison sentencing.[1]

Often the "subjects" (victims?) of these decisions are not the ones who designed or deployed the algorithm. Rather, the algorithm runs on behalf of a "principal" and is typically constructed to optimize that party's objectives.[2] Examples include feeds on social media sites, pricing or product decisions for online retail stores, and the above examples of job and loan applications, sentencing decisions, and more.

This imbalance is part of the impetus behind recent interest in FATE (Fairness, Accountability, Transparency, and Ethics), similarly FAT or FATML or FAT*[3], "Responsible AI", and so on. The idea is generally to require algorithmic decisionmaking to adhere to certain principles or standards -- just as we would expect from people, as if the principal made the decision about the subject directly.[4]

In particular, this post will discuss some of the background behind fairness in machine learning.

1. We'll cover a few ways things can go wrong when using learning algorithms to make decisions.
2. We will discuss conceptions of fairness at an abstract, philosophical level. What might we want from a "fair" algorithmic decisionmaking system?
3. We'll briefly mention settings where algorithms provide input to human decisionmakers.
4. We'll talk about algorithms making autonomous decisions and individual fairness.
5. We'll talk about common formalizations of group fairness.
6. We'll discuss causality and wrap up.

1. Ways things can go wrong

Deploying algorithmic decisionmaking can easily cause ethically problematic results.

• The training data can be biased, leading the algorithm to make biased decisions. For example, past data on criminal arrests and convictions in the U.S. is generally racially biased (in some sense I am not making precise here). It may be unfair to base future sentencing decisions on this data.
• The training data can appear unbiased, but the algorithm may nevertheless learn to make biased or unfair decisions. For example, if 70% of the visitors to a webpage are male, an algorithm might start optimizing for male audiences.
• Short-term decisions can have long-term, hidden, and complex effects. One example is feedback loops. An algorithm predicts crime in a certain neighborhood, so police send more patrols there than other places and discover more crime, leading the algorithm to predict even more crime there....

As with unconscious bias, these kinds of discrimination can be subtle or easy to miss -- at least to the person doing the discriminating -- need not be at all intentional, but can have large systematic effects.

2. Conceptions of fairness

There are many connotations to the English word "fairness". We're focusing on a decision regarding a person. Let's make it more precise - a decision y regarding a person who is described by features x. Here y comes from a set of possible decisions such as ads to show, approve/deny an application, release/not on bail. x represents the information available to the decisionmaker about the person. x might include credit score, browsing history, gender, race, previous convictions, employment status, or more (or less).

A first cut at defining fair decisions could be: everyone gets the same decision. This could be problematic for a few reasons. People might want different things. It might not be possible (e.g. college admissions, where only a certain number of slots are available). It might conflict with the objectives of the principal (e.g. loans should only be given to applicants who can repay).

Tony's adventures in fairness, part 1.

A subject-centric approach would be: give each subject the decision they most prefer. This is easiest to defend as an ethical ideal, but has pragmatic problems: as above, it may be impossible due to constraints, and may conflict with principal objectives. Also, the principal/algorithm might not even know what subjects want or be able to ask them. To simplify some of these challenges, researchers typically study settings in which there is an obviously desirable alternative and an undesirable one, for example, y=+1 if the loan is approved (or the applicant admitted, or released on bail) and y=-1 if denied (etc).

Tony learns about incentives.

A more principal-centric approach goes like this. The principal is hoping to accomplish some task, e.g. get a loan repaid or reduce crime. A fair approach is to choose the subjects who are objectively most qualified, e.g. have the best chance of repayment or lowest risk of committing a crime. This is sometimes called meritocratic fairness in the fairML literature. Note that in this case, we actually don't have any inherent conflict between fairness and accuracy/performance. If we could perfectly assess each applicant's "merit" and decide based on that, this would be considered fair by definition, and would make the decisionmaker happy too. So here the tension comes from our inability to perfectly assess merit. We might be worse at it for different groups, or we might make different kinds of mistakes for different groups.

Tony learns about lawsuits.

The notion of meritocratic fairness -- decide based only on merit -- is closely related to discrimination, which we might define as making decisions based on attributes of subjects that are unrelated to the nominal objective. In United States law, illegal discrimination is often categorized as either disparate treatment -- when the decisionmaking process explicitly treats different groups (e.g. race or gender) differently -- or disparate impact, when groups are apparently treated equally but one group is more negatively affected. We'll come back to these.

A final distinction that comes up is between a fair procedure versus a fair outcome. In computer science, being quantitative and measurement-based, we tend toward measures of fairness such as counts of outcomes (e.g. fraction of men accepted to college vs women, etc.). We focus less (perhaps wrongly) on the concept of a fair procedure, e.g. an application process in which every applicant has the chance to be considered fully and their merits taken into account (even if it leads to apparently-biased outcomes). This is somewhat similar to the disparate-treatment/disparate-impact distinction.

3. Algorithms as input

In important and high-stakes contexts, such as sentencing, algorithms are not likely to completely replace humans any time soon. Rather, information provided by algorithms will be inputs to human decisionmakers. For example, a judge deciding on bail or parole may take into account an algorithm's prediction or recommendation about a subject.

In this context, it's not clear what it means for the algorithm to be fair, since it is merely one cog in a machine. It could be that a seemingly-biased algorithm actually helps judges, who are aware of its weaknesses, make fairer decisions. This illustrates two general principles that arise in fairML contexts. (1) A prediction or decision often sits in a larger context. (2) Making an intermediate step "more" or "less" fair does not necessarily have the same impact on the system as a whole.

One implication: it's harder to define fairness for algorithms that only make predictions, not decisions. How are the predictions used? What happens when they change? Without knowing, "fairness" is meaningless[5].

So the cases where algorithms are just one input to a decisionmaking process are much harder to understand, formalize, or study theoretically. Of course, I'd also argue they are the most important as big decisions will generally continue to be made by humans, possibly with the help of algorithms.

4. Individual fairness in algorithmic decisions

Okay, let's consider an algorithm making fully automatic decisions. For now, let's assume a few restrictions on the setting that will make it easier to formalize fairness:

• The decision is binary: yes/no, approve/deny, accept/reject, etc.
• A "yes" decision is good or desirable for all subjects; a "no" is bad.
• The principal has an objective in mind, so we are interested in meritocratic fairness, i.e. preventing discrimination.

It's helpful to separate two types of fairness guarantees: individual fairness and group fairness.

In individual fairness, the idea is to guarantee every subject that they will be treated fairly as compared to other individuals. The main formalization of individual fairness, that I know of, is the "fairness through awareness" framework of Dwork, Hardt, Pitassi, Reingold, and Zemel (2011).[6] The idea is to define some similarity measure d(x1,x2) on subjects. Here x1,x2 is the information the algorithm has about subjects 1 and 2 respectively. If they are very similar, then d(x1,x2) is small (if identical, zero). Then we require that the more similar two subjects are, the more similar the algorithm's decision must be for them.

The problem of course is that the algorithm must decide yes or no for each person. So how can it comply with this fairness requirement? The usual approach is that the algorithm can be randomized. For each person x, it chooses a probability of yes and of no. Then if d(x1,x2) is small, we require the probabilities to be close.

As an example, applicants for a loan can be judged as similar based on their credit history, income, etc. By excluding things like age, race, and gender from the similarity measure, we disallow discrimination. Two people with similar credit histories and so on must be treated similarly regardless of other features.

The main problems with this definition seem to be pragmatic. How do we define the similarity measure exactly, and who gets to define it? A particular problem is that it is defined as a sort of "whitelist", specifying everything that may be used, rather than (as is more usual for something like legislation) a blacklist or list of features that may not.

5. Group fairness

In contrast to individual-level fairness we have various notions of group fairness. In group fairness, we usually consider some predefined groups such as ethnicities, genders, age groups, or so on. The concern is that, at a population level, one of these groups (say a certain race) are being discriminated against systematically. So we measure fairness by looking at the statistics of decisions given to different groups.

Going back to some of the philosophical and legal terms above, we can think of individual fairness as more of a procedural requirement (the process must be fair), while group fairness is more of an outcome-based or statistical requirement. Similarly, individual fairness is more like disallowing disparate treatment of different groups, while group fairness is more like disallowing disparate impact.

Here are some common measures used for group fairness. For concreteness, let's say we're just considering two racial groups, green people and blue people, and the question is approving visa permits to visit planet Earth. Imagine we can audit each decision to see if it was correct, i.e. whether the subject was "truly" qualified or not. (This assumes a meritocratic framework as discussed above. The maximally fair and accurate thing to do would be approving all the qualified candidates of both races, and no unqualified candidate.)

• Positive label rate. What fraction of blue people are approved? And what fraction of green people? One measure of fairness is how equal these are: if 60% of blues are approved and only 10% of greens, we may have discrimination against greens. This measure is sometimes considered too simplistic. What if a much larger fraction of blues are actually qualified for visas? Then the higher approval rate may be justified.
• Similarly, negative label rate (what fraction are denied?). Equal positive/negative label rates across both groups is sometimes called statistical parity or demographic parity.
• False negative rate. Of the blue people who are actually qualified, what fraction are rejected? For example, maybe 1/10 of qualified blue applicants are rejected but 3/4 of qualified green applicants are rejected. If the algorithm mistakenly rejects green people all the time but not blue, it may be discriminating against greens.
• Similarly, false positive rate. Thus some algorithms shoot for equalized false negatives and/or equalized false positives, sometimes also called equalized odds.
• Conditional error rate (of rejections). Of the blue people that the algorithm rejected, what fraction should actually be accepted? For example, maybe when the algorithm rejects a blue candidate, it's wrong 20% of the time, but when it rejects a green candidate, it is wrong 60% of the time. If the algorithm's recommendation to reject is usually right for blues but usually wrong for greens, it may be discriminating against greens.
• Similarly, conditional error rate of acceptances. Thus some algorithms try to achieve equalized conditional error rates. (I made this term up -- there doesn't seem to be a standardized name for this measure. It is closely related to calibration.[7])

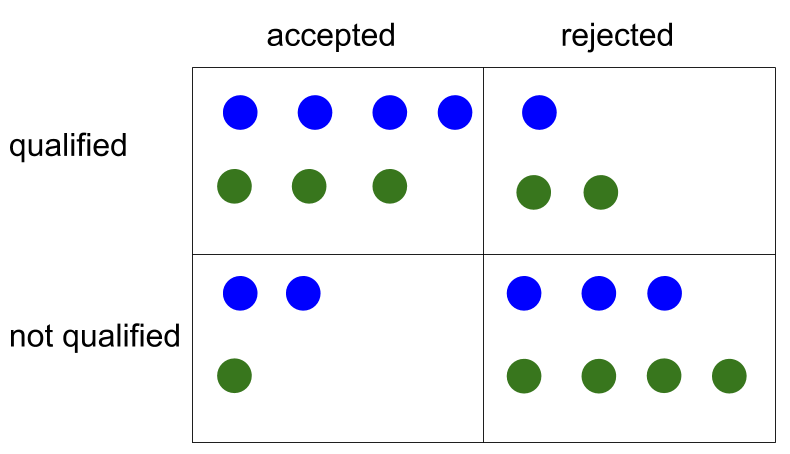
An example with 10 blue and 10 green people. 5 blue people are qualified, of which 1 is rejected, so the blue false negative rate is 1/5. The green false negative rate is 2/5. Meanwhile, 4 blue people are rejected, of which 1 was an incorrect decisions (1 was qualified), so a 1/4 conditional error rate of rejections. For greens, the conditional error rate of rejections is 2 out of 6, or 1/3.

Of course, these measures are in tension: you generally can't expect to satisfy more than one of them at a time. This was famously illustrated when ProPublica wrote a 2016 article[8] arguing that a criminal risk assessment tool, COMPAS, had a vastly different false negative and false positive rates for black people and white people. Black people who did not reoffend were much more often labeled high-risk than white people who did not reoffend. White people who did reoffend were much more often labeled low-risk.

The makers of COMPAS, Northpointe, responded that this was the wrong fairness metric.[9] They claimed that conditional error rate (as I define it above) was the right measure and argued that it was satisfied by COMPAS: when it labeled a black person as likely to offend, this was a mistake about equally as often as when it labeled a white person as likely to offend. The same went for those labeled unlikely to offend.

Of course, there is no technical resolution to this paradox, since it is impossible to generally satisfy both measures at once unless your predictor is perfect. One has to decide philosophically on which measure is important, and I don't know of any accepted arguments for these measures.

One take is that each measure -- false positive/negative rate and conditional error rate -- can be viewed as a Bayesian measure of the chance of facing a mistake, from two different perspectives. From the perspective of a random subject, say a green non-offender, the false negative rate can be interpreted as her belief about the chance of being falsely labeled as likely to offend. Equalized false negative rates requires that a green and blue non-offender face the same chances; otherwise the process is unfair.

From the perspective of a decisionmaker facing a green subject with label "likely to offend", the conditional error rate is the decisionmaker's belief about the chance this label was a mistake. Equalized conditional error rates requires that we make mistakes at the same rates on green and blue subjects. If we believe we are making more errors when labeling one race offenders than the other, then the process is unfair.

A final comment about group fairness: it seems insufficient, as it can be satisfied with procedures that are "obviously" unfair. For example, one can automatically reject every green applicant over 6 feet tall regardless of qualifications, yet still satisfy all the above notions. In general, I'm uneasy about group fairness because it seems to be Bayesian mostly from the algorithm's point of view, facing a random population of people. For each fixed person, the decision could be very arbitrary and unfair, yet as long as this unfairness "evens out" on average over the population, group fairness can be satisfied.

6. On causality and control

Let's go back to Tony's adventures in job hiring (cartoon). Hiring for a sales position based on height seems clearly unfair. But for an NBA team, hiring based partly on height might be considered fair. Why? One answer could be that in basketball, height has a causal influence on job performance. That is, making someone taller will, all else equal, improve their basketball potential. The same is not true, as far as we know, in sales or software engineering.

The interesting thing about the above example is that height is not under a person's control, but it can still perhaps be "fair" to use it in the hiring process. Similarly, consider zip code and bail decisions. Zip code is under someone's control (let us say), and it may also be highly correlated with crime, yet we may still be uncomfortable with basing bail on someone's zip code. I suggest the reason is again causality: regardless of whether the attribute is under the person's control, it is not fair to base decisions on it unless it is causally related to the outcome being measured.[10]

So causality gives one perspective on meritocratic fairness. A factor can be fair or unfair regardless of whether it is under a person's control, as long as it has a causal relationship to "merit" (in the sense of the meritocratic decisionmaking process).

Of course, machine learning has been so successful in part because of wringing good predictions out of correlations in the data. So maybe it's not surprising that it can be unfair.

The causal framework can also be abused, as Tony's hiring practices in the cartoon illustrate. A similar argument is used to justify e.g. practices like racial discrimination in hiring: something along the lines of "our customers are racist, so even if we aren't, hiring a certain race is bad for business." These scenarios go outside the "meritocratic" framework we've been discussing, because here (according to Tony or the business), "merit" or "performance" really are caused in part by unfair attributes like height and race. To address these issues, we must go outside this framework.

7. Other considerations

Before wrapping up, let's list a few other themes that tend to arise in fairML.

The transparency paradox. It might seem that discrimination can be avoided by not telling the decisionmaker any sensitive features, such as race. However, data generally contains features correlated with e.g. race, making it easy for algorithms to accidentally learn biased rules anyway. (See redlining.) In fact, many argue that the best way to achieve fairness is via complete transparency, i.e. give the algorithm access to as much data as possible including protected attributes, but then force the algorithm to correct for these biases manually ("greenlining").

Tyranny of the dataset-majority. Suppose we are training a simple recommendation system with a population that is 95% under 50 years old. It is quite likely to perform poorly on those over 50 simply due to fitting the preferences of a different population. One approach to fixing this is to ask for full transparency: if we know the ages of all users, we can train a completely separate system for people over 50. But do we train a separate system for each gender? Race? What about the extreme minorities in these groups? What if we don't have access to these attributes? The kind of unfairness that simply comes from fitting to error rate on the majority may be very common and hard to fix.

Decisionmaker: friend or foe? Regulations and legislature typically treat decisionmakers as adversaries and lay down rules to prevent them from discriminating. But computer scientists typically take the perspective of working for the decisionmaker and view her as "the good guy"[11]. So in line with the transparency paradox, they will often argue: let our algorithms access and utilize the protected attributes, and we will actually be able to make fairer decisions! Of course, the flip side is that an unscrupulous decisionmaker is also given more scope to make a complex algorithm that navigates this data to appear fair while actually being biased.

In other words, I suppose, computer scientists sometimes argue in favor of using disparate treatment as a tool to mitigate disparate impact. Perhaps this illustrates the CS perspective mentioned above that measurable "impact" outcomes are what matter for fairness, as opposed to process.

8. Wrapup

There are many aspects of fairness in ML that we've skipped. For example, biases in word embeddings and natural language processing ("man is to programmer as woman is to homemaker??"[12]); issues with facial recognition and racial or gender disparities; sociological, political, and philosophical angles; all kinds of problems with predictive policing[13]; and much more.

There's a ton of literature in this area and, while I've distilled down lessons from quite a bit of it, I've cited very little. It's a rapidly-growing area where few really good answers are yet known, and I think it's helpful and important to start a few steps back from the literature and think your way through the issues before diving into math. Anyway, you can find plenty of references at the FAT* conference linked below.

Okay - we've gotten to the end of the blog post and don't have any solutions, but we do have some perspective on chunks of what might be the problem. And I guess that's something.

Notes: