Useful Bounds via Taylor's Theorem
Posted: 2017-10-06.
In this post, we'll take a look at some common and useful bounds on the exponential and logarithm functions and see how they're derived using Taylor's Theorem.
Specifically, we'll show bounds like, for all $x \geq 0$, \begin{align*} 1-x &\leq e^{-x} \leq 1-x+\frac{x^2}{2} \\ x-\frac{x^2}{2} &\leq \ln(1+x) \leq x , \end{align*} and arbitrarily-tighter versions.
The Workhorse
The key tool we're going to use is Taylor's Theorem, which deals with approximating a function by a polynomial made up of its derivatives of various orders.
Taylor's Theorem (one useful form). Let $f: \mathbb{R} \to \mathbb{R}$ be $k+1$-times differentiable with all derivatives continuous. Fix $x_0$ and let \begin{align*} P_k(x) &= f(x_0) + f'(x_0)(x-x_0) + \ldots + \frac{f^{(k)}(x_0)}{k!}(x-x_0)^k \\ R_k(\xi;x) &= \frac{f^{(k+1)}(\xi)}{(k+1)!}(x-x_0)^{k+1}. \end{align*} Then $$ f(x) = P_k(x) + R_k(\xi;x) $$ for some $\xi$ lying between $x_0$ and $x$.
Note. $P_k(x)$ is interpreted as an approximation to $f$, while $R_k(\xi;x)$ is some "remainder".
More traditionally, this is taught as useful when bounds can be given on $|R_k(\xi,x)|$, as this implies that $P_k(x)$ is a good approximation to $f$. Here, we have a similar motivation but slightly different approach. Our goal will be to find upper or lower bounds on $f$, though of course we would prefer that they be reasonably close.
Corollary. If $R_k(\xi;x) \leq 0$ for all $\xi$ between $x_0$ and $x$, then $f(x) \leq P_k(x)$. Symmetrically, if $R_k(\xi;x) \geq 0$ for all $\xi$ between $x_0$ and $x$, then $f(x) \geq P_k(x)$.
The Exponential Function
Let's consider the function $e^x$, with Taylor series around $x_0=0$ of \[ 1 + x + \frac{x^2}{2} + \cdots + \frac{x^k}{k!} + \cdots \] as well as $e^{-x}$, which has \[ 1 - x + \frac{x^2}{2} - \cdots + (-1)^k\frac{x^k}{k!} + \cdots . \]
The first thing to figure out, when applying a bound or approximation, is the regime you're interested in. If you're dealing with $x=1000$, $x=10000$, or similar, then $e^x$ is just big -- what else do you want to say? (In this post, the bounds we derive will actually hold for arbitrarily large $x$, but they won't be very meaningful for $x$ bigger than $1$.)
But for small $x$, say $x \approx 0$, the function $e^x$ isn't so scary and it makes lots of sense to try to upper-bound or lower-bound it by more prosaic functions that might be easier to deal with.
$1+x$ is not such a great approximation to $e^x$ on a large range, but is when $x \approx 0$:
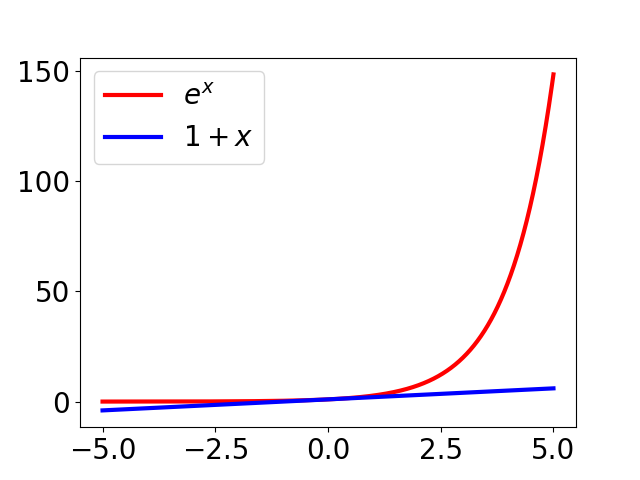
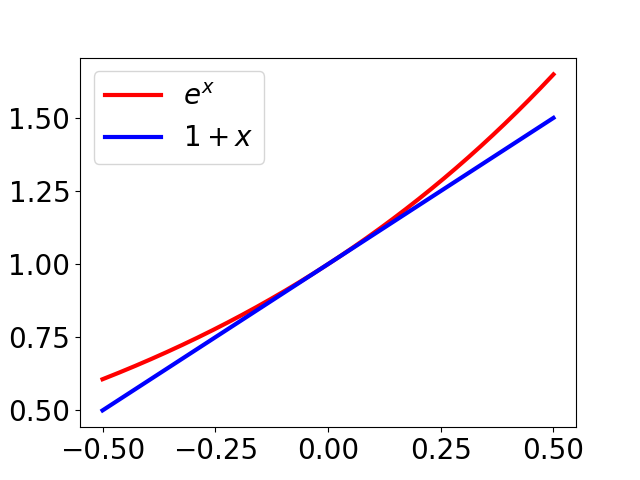
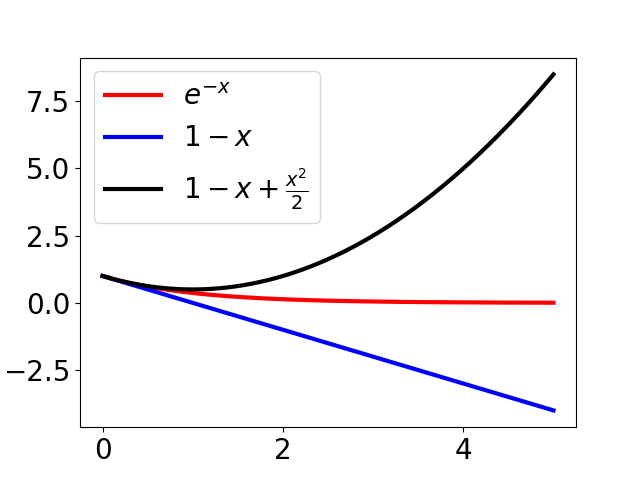
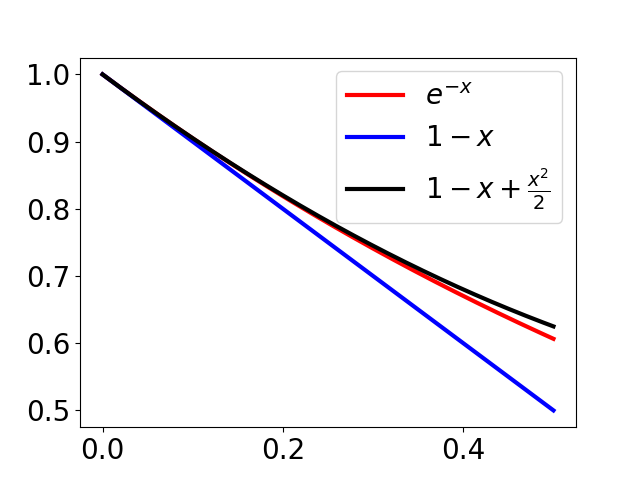
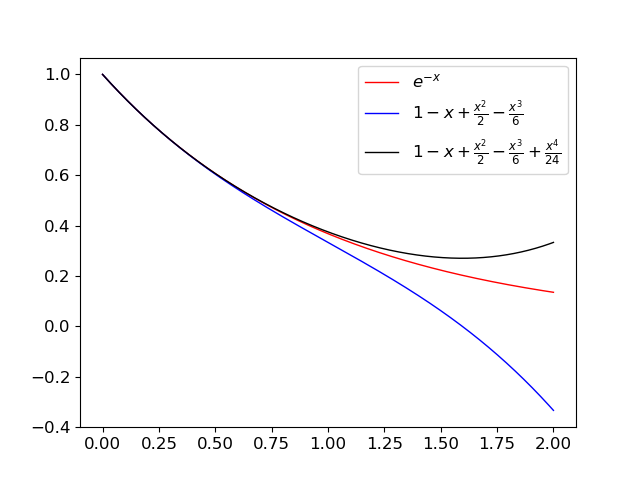
Similarly for $1-x+\frac{x^2}{2}$ and $e^{-x}$:
Note that our previous choice of $x_0 = 0$ makes sense since we're approximating or bounding our functions near zero. For $e^x$, we have $R_k(\xi;x) = \frac{1}{(k+1)!}e^{\xi} x^{k+1}$. Notice that for $k$ odd, $R_k(\xi;x) \geq 0$ for all values of $x$ and $\xi$. Given the corollary, this immediately says:
Bounds for $e^x$:
Fact. For all $x$, $1+x \leq e^x$.
Fact. For all $x$ and all odd $k$, $\sum_{j=0}^k \frac{x^j}{j!} \leq e^x$.
(Note this is not immediately obvious when $x$ is negative, at least, not to me.)
The bound for $1+x$ is often used with probabilities as follows: Suppose we have $n$ independent trials each with a probability $p$ of failure. Then the chance that they all succeed is the product of the probabilities: \begin{align*} (1-p)^n &\leq \left(e^{-p}\right)^n \\ &= e^{-pn}. \end{align*}
Speaking of smooth segues, sometimes in the above scenario we want a bound going the other way, i.e. to say that $e^{-x}$ isn't much bigger than $1-x$, at least near zero. For $e^{-x}$, we have $R_k(\xi;x) = (-1)^{k+1}\frac{1}{(k+1)!}e^{-\xi}x^{k+1}$. Focusing on positive $x$, we get $R_k(\xi;x)$ is positive (negative) when $k$ is odd (even).
Bounds for $e^{-x}$:
Fact. For all $x \geq 0$, \[ 1 - x \leq e^{-x} \leq 1 - x + \frac{x^2}{2} , \] and more tightly \[ 1 - x + \frac{x^2}{2} - \frac{x^3}{6} \leq e^{-x} \leq 1 - x + \frac{x^2}{2} - \frac{x^3}{6} + \frac{x^4}{24} , \] and so on.
Logs
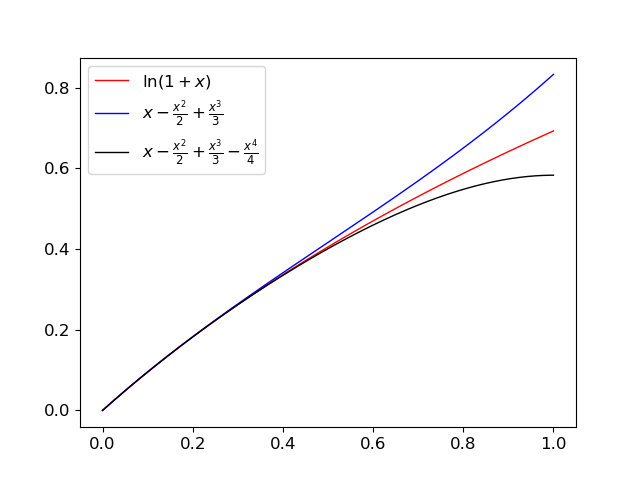
Our other example for today is $\ln(1+x)$, which has Taylor series \[ x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots + (-1)^{k-1} \frac{x^k}{k} + \cdots . \] Again, we're interested in the regime where $x$ is close to zero, and this is the Taylor series around $x_0=0$; notice that the $k$th derivative of $\ln(1+\xi)$ is $(-1)^{k-1}\frac{(k-1)!}{(1+\xi)^k}$.
Here $R_k(\xi;x) = (-1)^{k}\frac{1}{(k+1)(1+\xi)^{k+1}} x^{k+1}$. Focusing on positive $x$ for simplicity (which implies $\xi$ is positive as well), we get $R_k(\xi;x)$ is negative for odd $k$ and positive for even $k$. So odd terms give upper bounds, and even terms give lower bounds.
Bounds for $\ln(1+x)$:
Fact. For all $x \geq 0$, \[ x - \frac{x^2}{2} \leq \ln(1+x) \leq x , \] and more tightly \[ x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} \leq \ln(1+x) \leq x - \frac{x^2}{2} + \frac{x^3}{3} , \] and so on.
Exercise. Show that the upper bounds on $\ln(1+x)$ above hold for all $x \gt -1$.


Comments