Convex Duality

Posted: 2016-10-20.

Every convex function has a special relative (or perhaps "evil twin") called its conjugate or dual. In this post, we'll walk through the definition both formally and visually.

Don't forget to brush up on convexity first!

Dual Spaces

A very cool concept in analysis is that of dual spaces (as opposed to the "duel spaces" originally explored by Galois). (Ouch ... too soon?)

Suppose we are given a vector space $V$. We'll focus on $V = \mathbb{R}^n$ for simplicity and concreteness, but I'll start with the more general notation to emphasize that greater generality is also possible below if you want it.

Now let $V^*$ be the set of all linear functions from $V$ back to the underlying field, in our case $\mathbb{R}$. These are all functions $g$ where $g(\alpha x + \beta x') = \alpha g(x) + \beta g(x')$. It turns out $V^*$ is also a vector space, and it is called the dual space to $V$. Note you should be thinking of linear functions $g$ as elements of this space. For example, given $g_1, g_2 \in V^*$, then $\alpha g_1 + \beta g_2$ is also in $V^*$, and it is the linear function $x \mapsto \alpha g_1(x) + \beta g_2(x)$.

Note in $\mathbb{R}^n$ this is all so easy that it's automatic: We can associate any linear function $g: \mathbb{R}^n \to \mathbb{R}$ with a vector $v_g \in \mathbb{R}^n$ with $g(x) = \langle v_g, x \rangle$. So for $V = \mathbb{R}^n$, the dual space $V^*$ is also $\mathbb{R}^n$. But I want to think of vectors $x^* \in V^*$ as being linear functions on $V$.

By the way, as this might suggest, for finite-dimensional vector spaces, the double dual is the original space -- i.e. $V^{**} = V$. This can be interpreted, if you're so inclined, as thinking of $x \in V$ as linear functions of elements $g \in V^*$, where $x: g \mapsto g(x)$.

One more prerequisite: an affine function is a linear function plus a constant. So for example we can write an affine function $g: V \to \mathbb{R}$ as $\langle x^*, x \rangle - \mu^*$ where $x^* \in V^*$ and $\mu^* \in \mathbb{R}$.

Diving In

Suppose we are given a convex function $f: V \to \mathbb{R}$, where $V = \mathbb{R}^n$, that is also closed: its epigraph $F$ is a closed set. (An equivalent but way less elegant condition on $f$ is called "lower semicontinuity", and I hate that I even had to mention such an ugly term for something so clean.)

Here are two ways to describe $f$ in terms of sets:

• The set of points in the epigraph $F$.
• The set $F^*$ of affine functions lying below $f$, i.e. \[ F^* = \left\{(x^*, \mu^*) : \forall x, f(x) \geq \langle x^*, x\rangle - \mu^* \right\} . \]

We can describe $f$ by listing all the points above it (its epigraph $F$) or equivalently (below), all affine functions lying below it (call them $F^*$).

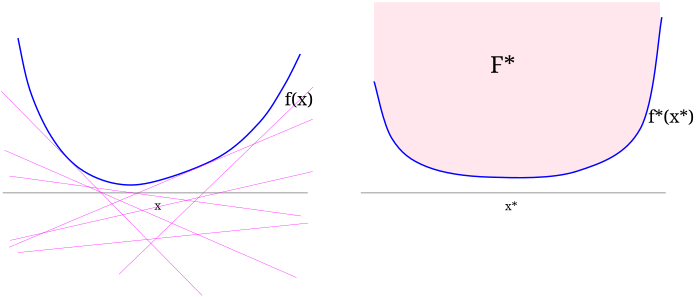
Above: $F^*$ turns out to be the epigraph of a convex function $f^*$ defined on the dual space.

Below: the affine functions lying below $f^*$ make up the original epigraph $F$.

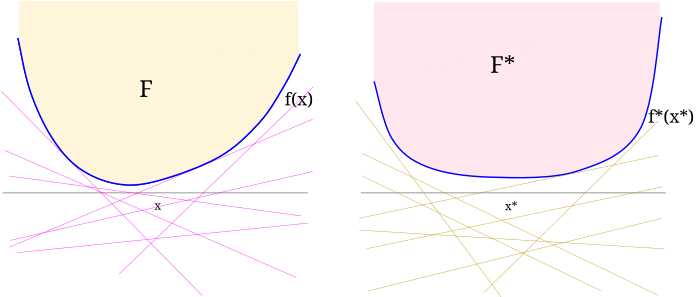
Now my claim is that $F^*$ is the epigraph of a convex function $f^* : V^* \to \mathbb{R}$. Meanwhile, we can interpret $F$ as a set of affine functions $g: V^* \to \mathbb{R}$ that lie below $f^*$.

Exercise 1. Prove that $F^*$ is a closed convex set.

Exercise 2. Show that there exists a function $f^*: V^* \to \mathbb{R}$ whose epigraph is $F^*$; conclude that $f^*$ is a closed, convex function. (Hint: $f^*$ had better map $x^*$ to the smallest $\mu^*$ such that $(x^*, \mu^*) \in F^*$; just show this is well-defined!)

Although I'm being a bit sloppy and omitting it, notice that the domain of $f^*$ will consist of (the convex hull of) the subgradients of $f$. Also, we haven't worried about what happens if $f$ is not closed -- feel free to investigate on your own!

Tangents

Notice you can view $F$ and $F^*$ as "dual" sets in that, given $F$, we can define \[ F^* = \left\{ (x^*,\mu^*) ~:~ \forall (x,\mu) \in F, \mu + \mu^* \geq \langle x, x^* \rangle \right\} . \] (Of course, given $F^*$, you can define $F$ exactly analogously.) In a sense, $f$ and $f^*$ define the "tight" boundaries where this optimization / inequality is closest.

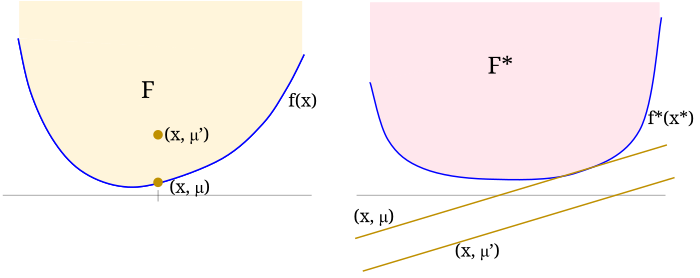
$f$ and $f^*$ describe the extremal points of the sets $F$ and $F^*$. Here $(x,\mu')$ lies in the interior of $F$ and the corresponding affine function $\langle x, \cdot\rangle - \mu'$ lies strictly below $f^*$. But $(x,\mu)$ lies on the boundary of $F$ (lies on $f$) and the corresponding affine function is tangent to $f^*$.

For any $(x^*,\mu^*) \in F^*$, we can rearrange the definition of $F^*$ to say \begin{align} \mu^* &\geq \langle x^*, x\rangle ~ - ~ f(x) \qquad (\forall x) \\ \iff \mu^* &\geq \sup_x ~ \langle x^*, x \rangle ~ - ~ f(x) . \end{align} Since $f^*(x^*)$ is defined to be the minimal $\mu^*$ for which this holds, \[ f^*(x^*) = \sup_x ~ \langle x^*, x \rangle ~ - ~ f(x) . \] Furthermore - and this is important - the $x$ that achieves this supremum will be a subgradient of $f^*$ at $x^*$. (See the next figure.) Similarly, \[ f(x) = \sup_{x^*} ~ \langle x^*, x \rangle ~ - ~ f^*(x^*) \] with this supremum achieved at $x^*$ a subgradient of $f$ at $x$.

$f$ and $f^*$ give a correspondence between points $x \in V$ and $x^* \in V^*$, where $x^* \in df(x)$ and $x \in df^*(x^*)$.

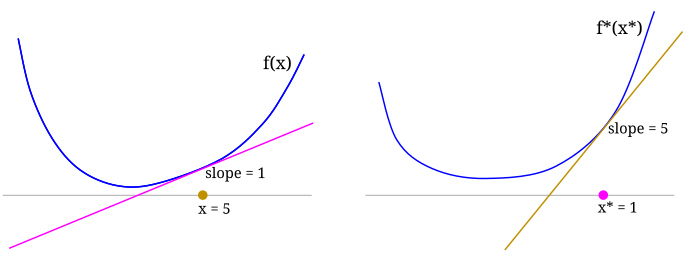
Below: points $x$ on the left are slopes of tangents on the right; points $x^*$ on the right are slopes of tangents on the left.

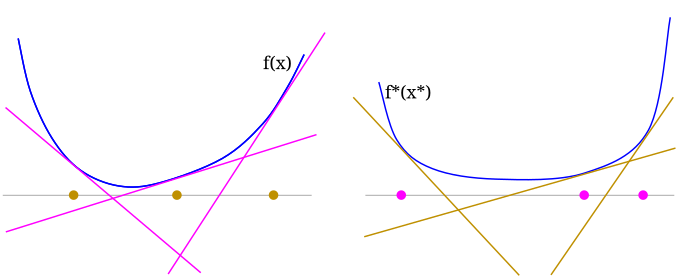
It's worth restating / collecting these:

Examples

Here are some examples generated by this python code.

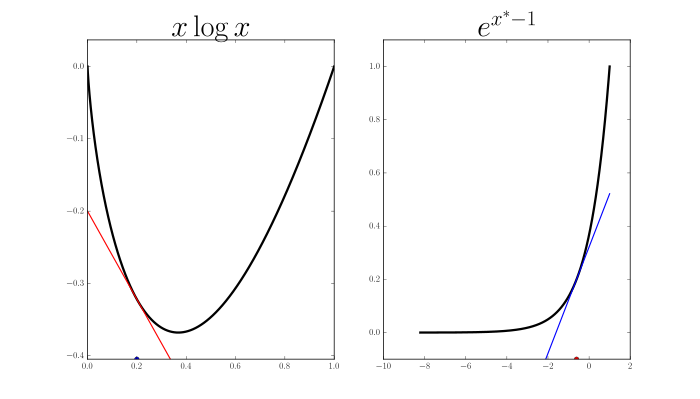
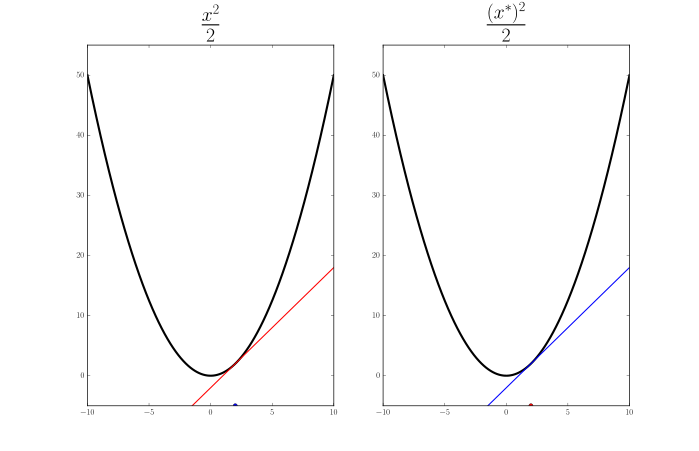
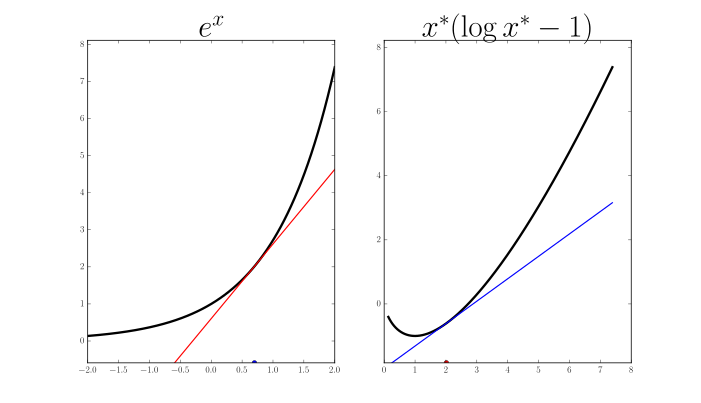
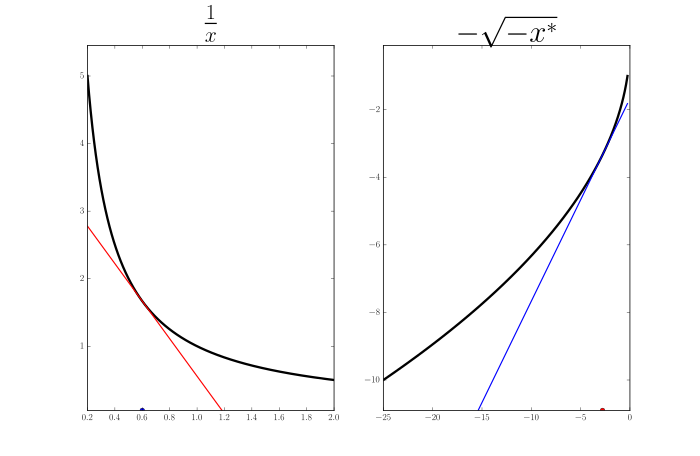
One-dimensional examples. Plots of some example $f$ (left) and their conjugates $f^*$ (right). Here $x$ and $x^*$ are just scalars. On each figure, I show one corresponding pair $x, x^*$ where $x$ is a red point on $f$'s plot and a red tangent line (slope) on $f^*$'s plot; $x^*$ is a blue slope on $f$'s plot and a blue point on $f^*$'s plot.

Two-dimensional examples. More conjugate pairs $f$ (left) and $f^*$ (right). Now $x, x^* \in \mathbb{R}^2$. Again, I try to show a corresponding pair $x, x^*$ where $x$ is a point on $f$'s plot and a tangent plane on $f^*$'s plot; $x^*$ is a plane on $f$'s plot and a point on $f^*$'s plot.

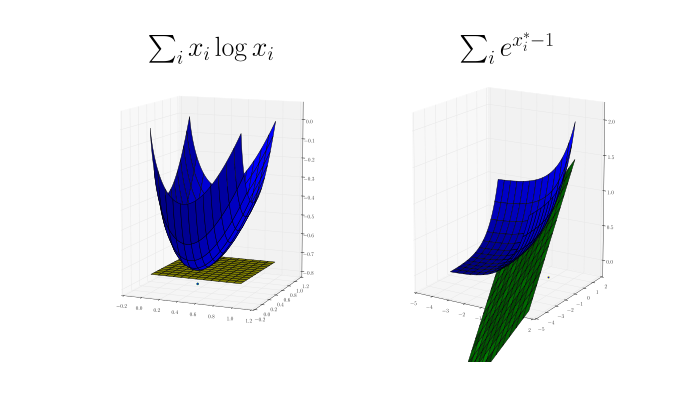
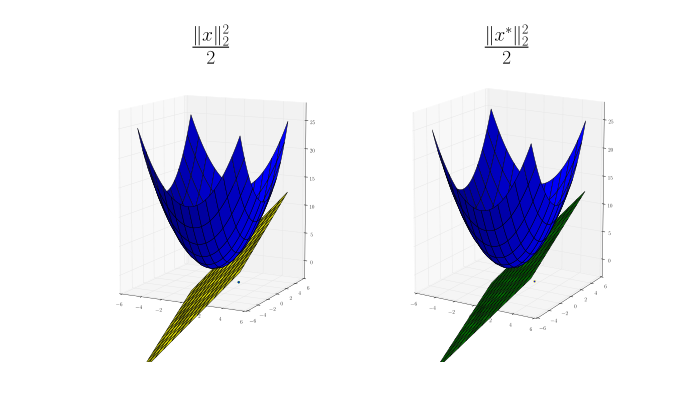
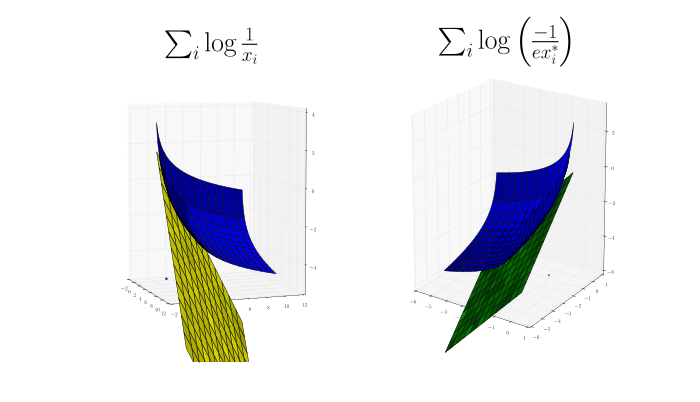
Exercise 3.
Find the conjugate of the function $x \mapsto \frac{1}{p} \sum_i |x_i|^p$ for $p \geq 1$.

Exercise 4.
You may have noticed from the figures above that $x \mapsto \frac{1}{2}\|x\|_2^2$ is its own conjugate. Prove that it is the unique function for which this holds. (Easy mode: prove it is the unique differentiable one.)

Exercise 5.
Let $f^*$ be conjugate to $f$ and $x, x^*$ and $y, y^*$ be conjugate points. Show that $D_f(x,y) = D_{f^*}(y^*, x^*)$ where $D_f$ is the Bregman divergence of $f$.